[理知논술/날아오르는 창의사고력]카메라를 통해 보는 수학

과거에 카메라는 특별한 날을 기념하기 위해 가끔 꺼내 쓰는 물건이었다. 자연히 한 가정에 한 대 정도 가지고 있는 게 보통이었다. 최근에는 가족 구성원마다 한 대씩 카메라를 가지고 있는 경우가 많다. 휴대전화에 딸린 카메라 기능까지 포함하면 한 사람이 몇 개의 카메라를 쓰는 일도 흔하다.

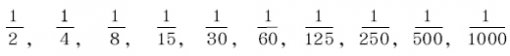
사진을 찍는 일은 이제 특별한 일이 아니라 일상생활이 됐다. 사진 찍는 것을 좋아하는 사람들은 계절마다 카메라를 들고 여기저기 다닌다. 카메라의 원리를 따로 공부해서 다양한 구도로 멋진 작품을 만들어내기도 한다.

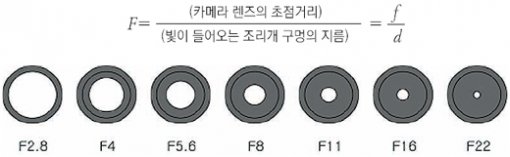
카메라를 능숙하게 다루려면 몇 가지 용어를 알아야 한다. 이런 용어들은 대부분 수학과 관련이 있다. 그중 빼놓을 수 없는 것이 ‘F수(혹은 f Number)’로, 흔히 ‘조리개값’이라고 한다. F수는 F=(초점길이)/(구경길이)와 같은 공식에 의해 얻어진다. 예를 들어 초점길이 100mm에 구경이 10mm이면 F=10이고 초점길이 100mm에 구경이 20mm이면 F=5가 된다. 여기서 알 수 있듯이 같은 초점길이에 대해 구경의 크기에 따라 F수가 작아진다. 즉, F수가 작으면 작을수록 구경이 커진다는 것을 알 수 있다.

원형구도, 사선구도, 삼각구도, 황금분할구도 등 다양한 구도를 잡을 때도 수학적 요소가 힘을 발휘한다. 다음 문제를 풀면서 사진 찍기에 담긴 수학적 의미를 발견해 보자.

김형진 영재사관학원·수학영재만들기 대표원장

수동카메라의 조리개 수치 F는 왜 √2배씩 늘어날까

▒ 문제 1

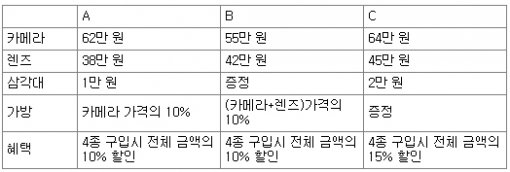
사진 찍는 것을 좋아하는 규현이는 DSLR 카메라를 구입하려고 합니다. 저렴하고 좋은 카메라를 구입하기 위해 카메라 가게 여러 곳을 돌아다녔습니다. 규현이가 원하는 모델의 카메라와 렌즈는 세 곳에서 팔고 있었는데, 가격은 다음과 같았습니다.

A, B, C 세 가게 중 한 곳을 선택하여 카메라, 렌즈, 삼각대, 가방 4가지 물품을 모두 구입하려고 합니다. 어느 곳에서 구입하는 것이 가장 저렴한지 구하시오.

【선생님의 도움】

① 계획하기

A, B, C 가게에서 구입할 때, 사야 할 4가지 물품의 가격과 할인받는 가격을 계산하여 지불해야 하는 비용이 최소인 가게를 선택합니다.

② 실행하기

ⅰ) A 가게

62+38+1+62×0.1=107.2(만 원), (할인)=107.2×0.1=10.72(만 원)

∴ 107.2―10.72=96.48(만 원)

ⅱ) B 가게

55+42+(55+42)×0.1=106.7(만 원), (할인)=106.7×0.1=10.67(만 원)

∴ 106.7―10.67=96.03(만 원)

ⅲ) C 가게

64+45+2=111(만 원), (할인)=111×0.15=16.65(만 원)

∴ 111―16.65=94.35(만 원)

따라서 C 가게에서 구입하는 것이 가장 저렴합니다.

③ 반성하기

할인을 제외했을 때, 가장 저렴한 곳을 찾아봅니다.

「문제2∼3

요즘 많이 사용하는 카메라는 자동 기능을 설정할 수 있어 초점이나 거리를 조정할 필요 없이 셔터만 눌러도 편리하게 사용할 수 있습니다. 그런데 규현이가 구입한 수동 카메라는 초점 거리를 일일이 조정해야 하는 것은 물론이고, 날씨의 맑고 흐림에 따라 F 값이라는 것을 조절해야 합니다. F 값은 카메라의 렌즈를 둘러싸고 있는 둥근 원통 모양의 겉면에 1.4, 2, 2.8, 4, 5.6, 8, 11 등과 같이 쓰여 있는 수를 말합니다.

첫 번째 수 1.4는 다름 아닌 √2의 근삿값이고, 그 다음 수들은 √2씩 곱해 나간 수들의 근삿값입니다. 이 수들은 카메라로 사진을 찍을 때의 빛의 양을 조절하는 조리개의 수치를 나타냅니다. 조리개란 카메라에 빛이 들어오는 통로의 크기를 조절하는 역할을 하는 장치로 F 값이 커질수록 빛의 양은 ½배씩 줄어듭니다. 이때, 조리개가 열린 정도를 나타내는 수가 바로 F 값으로 F 값은 다음과 같이 정해집니다.

셔터 속도는 조리개가 열려 빛이 들어오는 시간을 말하며, 다음과 같이 약 ½배씩 짧아집니다. 즉, 셔터 속도가 ½배만큼 짧아지면 빛의 양은 Z배씩 줄어듭니다.