[이지스터디]한문제를 풀어도 여러 각도에서 분석 또 분석!

문제해결력, 풀이법 연습한다고 더 많은 문제 푼다고 저절로 커질까

《많은 학생이 수학을 어렵게 느낀다. 특히 생소한 문제가 나오거나 아는 공식을 이용했는데도 문제가 풀리지 않으면 당황하는 경우가 적지 않다. 이런 현상이 나타나는 이유는 뭘까. 이는 단순히 풀이방법을 익히거나 정답을 맞히는 데 중점을 둔 학습 결과로 해석된다. 수학 지식과 주어진 조건을 이용해 문제를 분석하는 시간을 충분히 갖지 못한 학생들은 심화문제를 푸는 데 더욱 어려움을 겪을 수밖에 없다.》
다음 문제를 살펴보자.

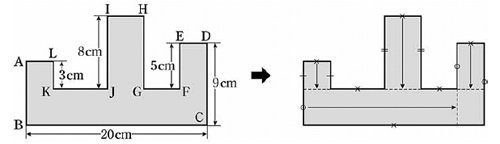
이 문제는 도형의 둘레 길이를 구하는 문제다. 변 AB, DE, FG, GH, HI, JK, LA의 길이는 나와 있지 않다. 하지만 오른쪽 그림과 같이 적당히 변을 이동하면 주어진 변의 길이를 이용해 도형의 둘레 길이를 구할 수 있다. 즉, 이 도형의 둘레 길이는 변의 길이가 20cm짜리 2개, 9cm짜리 2개, 8cm짜리 2개, 3cm짜리 2개의 합과 같다. 따라서 이 도형의 둘레 길이는 (20+9+8+3)×2=80(cm)이 된다.

또 다른 문제를 살펴보자.

===

A, B, C 3가지의 음료수가 있다. A 3병, B 7병, C 1병을 모두 사는 데는 3150원이 필요하고 A 4병, B 10병, C 1병을 다 사는 데는 4200원이 필요하다. A, B, C를 각 1병씩 사려면 얼마가 필요한가?

===

A, B, C의 가격을 각각 A, B, C라 하고 식을 세워 풀어보자.

왼쪽의 두 식으로 A, B, C 각각의 값을 구하려고 한다면 결코 이 문제를 해결할 수 없을 것이다. 위의 도형 문제에서 사용한 방법을 적용해 보자. 이 문제는 A, B, C 각각의 값을 구하지 않고 A+B+C가 나오도록 두 식 ㉠, ㉡을 적당히 변형해 해결할 수 있다. 오른쪽 식과 같이 ㉠을 3배하고 ㉡을 2배해 빼면 A+B+C=1050(원)이 나온다.

사진제공 시매쓰

앞의 두 문제는 형태는 서로 다르지만 비슷한 방법으로 풀 수 있음을 알 수 있다. 이처럼 문제의 형태나 영역에 관계없이 문제를 어떻게 풀어야 할지를 고민하는 과정에서 해결방법을 찾아낼 수 있다.

문제해결력을 기르기 위해선 한 문제라도 깊이 있게 여러 각도에서 생각해보는 것이 필요하다. 특정 풀이방법을 연습한다거나 많은 문제를 푼다고 해서 문제해결력이 길러지는 것은 아니다. 학교 성적에 만족하지 않고 좀 더 큰 목표를 가진 학생이라면? 지속적인 사고과정을 통해 문제해결력을 키우고 어려운 문제도 꾸준히 풀어보는 것이 좋다.

최보나 시매쓰수학연구소 책임연구원