[理知논술]논술에 강한 수학

가로선 가지가 아무리 많아도

일반적인 사다리타기는

왜 항상 1 대 1 대응일까

누구나 한 번쯤은 ‘사다리 타기’를 해봤을 것이다. 오늘은 ‘사다리 타기’에 대해 생각해보기로 하자. 우선, 사다리 타기의 규칙을 생각해보자. 사다리는 아무렇게나 타는 것이 아니다. 무조건 밑으로 내려가는 것이 아니라 옆으로도 가고 아래로도 가는 사다리만의 규칙이 있다. 이 규칙을 자세히 정의하기 위해 사다리를 분석해보자. 사다리 타기에서 아래로 내려오는 선을 ‘줄기’라고 하고, 줄기끼리 이은 선을 ‘가지’라고 하자. 그러면 사다리 타기의 규칙은 다음과 같이 정의된다.

1. 줄기를 타고 아래로 내려간다.

2. 가지를 만나면 가지 위로 이동한다.

3. 다시 줄기를 만나면 줄기를 따라 아래로 이동한다.

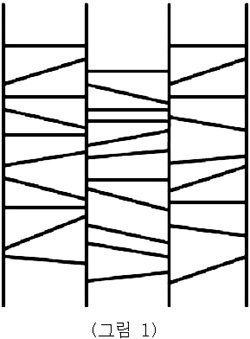
이렇게 사다리 타기의 규칙을 정의할 수 있다. 그런데 사다리 타기에서 우리가 생각해야 할 점은 무엇인가? 한 개의 선택사항이 유일하게 한 개의 결과 값에만 연결되는가? 또한 한 개의 결과 값은 유일한 선택사항에서만 도출되는가? 즉, ‘일대일 대응’ 관계가 성립하는지 여부다. 다음 (그림 1)을 보자.

이렇게 복잡한 사다리타기에서도 일대일 대응 관계는 유지되는가? 다음 (그림 2)와 같은 평범하지 않은 사다리 타기의 예도 살펴보자.

(그림 2)는 대부분의 학생이 처음 보는 사다리 타기일 것이다. 이런 종류의 사다리는 어떻게 탈까? 각 영문자는 두 개씩 있다. 한 쌍의 영문자가 서로 연결되어 있다고 생각하면 된다. 즉, A로 들어갔다면 다른 A로 나와서 계속 사다리를 타면 되는 것이다. 자, 이런 사다리 타기에서도 일대일 대응은 유지되는가?

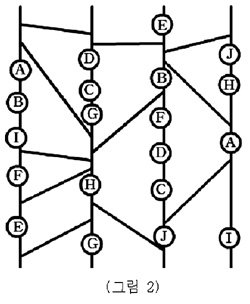
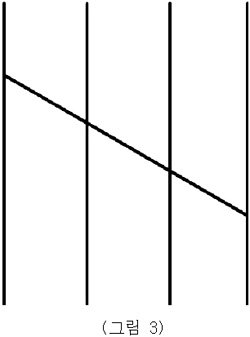
(그림 1), (그림2)의 사다리 타기는 일대일 대응이 유지된다. 그러나 다음 (그림3)을 보면 알 수 있듯이 항상 일대일 대응관계가 유지되는 것은 아니다.

그럼 이제 우리의 의문을 정리해보자.

1. 어떤 조건일 때 사다리 타기는 일대일 대응이 성립되지 않는가?

2. 일대일 대응인 사다리 타기를 ‘일반적인 사다리’라고 부를 때 ‘일반적인 사다리’는 왜 항상 일대일 대응인가?

두 질문에 대한 답을 구하기 위해 우선 2번 질문부터 해결해 보자. 지난 지면을 통해 우리는 ‘단순화’라는 것을 배웠다. 이 경우에도 마찬가지다. 세상의 모든 사다리 타기는 무한하다. 따라서 모든 경우를 시행해 보고 ‘사다리 타기는 일대일 대응이다’라고 증명할 수가 없는 것이다.

가장 단순한 사다리는 가지가 없는 사다리일 것이다. 이 때는 명확히 ‘사다리 타기는 일대일 대응이다’라고 말할 수 있다. 이번에는 줄기만 있는 기본형 사다리에 가지 한 개를 그려보자. 이 경우에는 어떤 변화가 생기는가? 가지로 이어진 두 줄기 사이에서 ‘선택사항’ 두 가지가 교환된다. 일대일 대응의 관계 속에서 두 개체만이 일대일 교환되었으므로 전체 일대일 대응 관계는 유지된다. 따라서 아무리 많은 가지(심지어 (그림 2)와 같은 이상한 가지)를 그리더라도 사다리 타기는 일대일 대응인 셈이다.

그렇다면 이제 2번 질문에 대한 답을 생각해보자. 일대일 대응이 성립되지 않으려면 어떤 가지를 그리면 되겠는가? 일대일 교환이 일어나지 않는 가지일 것이다. 즉 (그림 3)에 있는 가지처럼 가지끼리 이어져 있거나, 가지가 서로 교차될 때는 일대일 교환이 일어나지 않는다. 사다리를 타는 사람의 마음에 따라 몇 가지 경로가 생기게 되고, 이는 일대일 대응관계를 깨버리는 것이다.

안성환 ㈜엘림에듀 집필위원