[理知논술]초등생 생각하는 수학

시도교육청·대학 부설 영재교육원 초등부 선발시험 대비 문제(3∼5학년)

해설 및 정답은 인터넷 이지논술 사이트(www.easynonsul.com)에서 볼 수 있습니다.

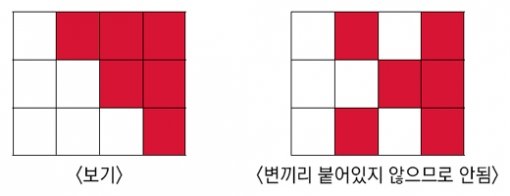
1. [도형] 12개의 작은 정사각형으로 이루어진 직사각형이 있습니다. 6개의 정사각형에 색칠을 하여 색칠한 부분과 색칠하지 않은 부분이 똑같은 모양이 되도록 만들 수 있는 서로 다른 모양은 <보기>를 제외하고 모두 몇 가지가 더 있는지 구하시오. (단, 색칠한 작은 정사각형들은 반드시 변끼리 붙어 있어야 하며, 반대로 색칠한 것은 같은 것으로 봅니다.)

Tip. 똑같은 모양이 되도록 하려면 작은 정사각형을 <보기>에 주어진 원래의 위치와 대칭이 되는 곳으로만 옮겨야 합니다.

2. [수와 연산] <보기>에 주어진 식을 잘 보고, ★ 기호가 나타내는 연산 법칙을 찾아 다음을 계산하시오.

〈보기〉 3★1=4 3★2=11 3★3=30 3★4=85

(1) 3★6 (2) 2★5 (3) (2★3)★2

Tip. ★은 곱셈과 덧셈을 이용한 계산 규칙입니다.

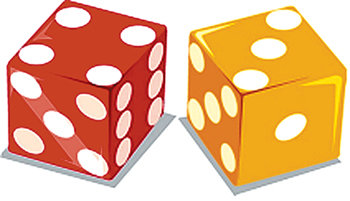
3. [확률과 통계] 다희와 소정이는 각각 주사위를 2번 던져서 나온 눈의 수로 수를 만듭니다. 같은 눈이 나오면 1을 만들고, 다른 눈이 나오면 두 눈의 수를 분모, 분자로 하는 진분수를 만듭니다. 주사위를 1번 던졌을 때 다희는 4가 나오고 소정이는 2가 나왔습니다. 각자 주사위를 한 번 더 던질 때, 다희가 소정이보다 작은 수를 만드는 경우는 모두 몇 가지가 있습니까?

Tip. 두 학생이 만들 수 있는 수를 모두 찾고, 각 경우에 대해 수의 크기를 비교해 보세요.

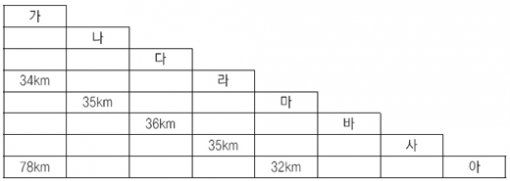
4. [문자와 식] 다음 표는 가, 나, 다, 라, 마, 바, 사, 아 8개의 기차역 사이의 거리를 나타낸 것입니다. 예를 들어, 가 역에서 라 역까지의 거리는 34km입니다. 가 역에서 아 역까지의 거리가 78km일 때, 라 역과 마 역 사이의 거리를 구하시오.

Tip. 주어진 역 사이의 거리를 이용하면 인접한 역 사이의 거리를 구할 수 있어요.

5. [규칙성과 함수] 아래 그림과 같이 화살표를 따라 □ 안에 차례로 번호를 써 넣었습니다. 마지막 □안에 들어갈 번호는 무엇입니까? (단, 세 줄에 있는 □의 개수는 서로 같습니다.)

Tip. 46번부터 151번까지 사각형의 개수는 각 줄에 있는 사각형 개수의 두 배가 됩니다.

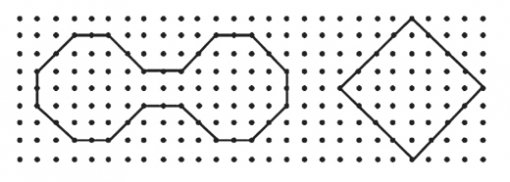
6. [측정] 다음 그림은 가로, 세로가 1cm 간격으로 점이 찍힌 종이 위에 두 도형을 그린 것입니다. 두 도형의 둘레의 차이가 가cm, 넓이의 차이가 나cm²라 할 때, 가+나의 값을 구하시오.

Tip. 가로, 세로 각각 1cm인 단위 정사각형을 기준으로 두 도형을 이루는 변과 대각선의 개수를 비교하여 둘레의 차이를, 정사각형의 개수를 비교하여 넓이의 차이를 구할 수 있어요.

7. [수와 연산] 다음 식을 계산한 값은 얼마입니까?

『(2+4+6+…+2006+2008)-(1+3+5+…+2005+2007)』÷2

Tip. 짝수끼리 모여 이루어진 덧셈식을 홀수에 관한 식으로 변형하는 방법을 생각해 보세요.

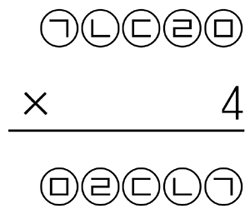
8. [문자와 식] 다음 곱셈식에서 ㉠∼㉤은 각각 다른 숫자를 나타냅니다. ㉢에 알맞은 숫자는 어느 것입니까?

Tip. 계산 결과가 다섯 자리 수이므로 ㉠은 1 또는 2입니다.

9. [통합형 심층] 1부터 18까지의 18개의 자연수를 두 개씩 묶어서 9쌍을 만들어 각 쌍에 있는 두 수의 합이 각각 어떤 자연수를 제곱한 수가 되도록 하려고 합니다. 이런 9쌍의 수를 모두 구하시오.

Tip. 1부터 18까지의 자연수 중에서 두 수의 합이 어떤 자연수의 제곱이 되는 쌍을 모두 찾아 보세요.

10. [통합형 심층] 영호는 1부터 9까지의 서로 다른 5개의 숫자를 차례대로 배열하였습니다. 영호는 친구에게 서로 다른 5개의 숫자를 차례대로 쓰라고 한 후, 오른쪽 <보기>와 같이, 영호가 쓴 수와 같은 수가 같은 위치에 있으면 ○, 같은 수가 다른 위치에 있으면 ×를 개수만큼 표시하고 같은 수가 없으면 아무 표시도 하지 않았습니다. <다음>은 친구들이 쓴 숫자 옆에 영호가 쓴 수와 비교하여 <보기>와 같이 표시한 것입니다. 영호가 쓴 숫자를 □□□□□에 차례대로 써 넣으시오.

Tip. (1)∼(4)를 활용하여 5개의 숫자를 먼저 알아내고, 그 다음 숫자들의 위치를 생각하세요. (2)를 통해 5, 6, 7, 8, 9 중 2개, 1, 2, 3, 4 중 3개가 있다는 것을 알 수 있어요.

김화자·하늘교육 선임연구원

▶easynonsul.com에 동영상 강의