공유하기
[理知논술/중학생 수리 논술]논리사고력으로 수학적 안목을
-
입력 2007년 10월 8일 03시 00분
글자크기 설정





그중 수학적 논리사고력을 중시하는 가장 큰 이유는 급변하고 다양화하는 미래 사회에 적응할 수 있는 힘을 길러 주기 때문이다. 진정한 수학적 힘은 단순 계산 능력이 아니라, 사고력을 바탕으로 주어진 상황을 해결하는 능력에 있는 것이다. 이런 이유로 최근 학생과 학부모 사이에서 ‘수학적 논리사고력’에 대한 관심이 높아지고 있다.
우리나라 교육도 종전의 공식 위주 암기 교육에서 벗어나 사고력 중심 교육의 시대로 접어들었다. 전통적인 학습은 간단한 수학적 사실을 이해하고 활용하는 측면에서 그쳤으나 이제는 수학적 개념, 원리, 법칙을 통해 수학적 지식을 학생 스스로 탐구, 발견하고 창조하는 능력을 기르기를 요구한다.
이러한 능력은 구구단을 외우기 시작하면서 얻어지는 것은 아니지만 수학과 현상에 대한 인내와 관심으로 충분히 얻을 수 있다. 그러기 위해서는 우선 수학적 흥미와 자신감을 가져야 한다. 자기 주도적인 학습과 스스로 탐구하는 능력을 기르는 것도 중요하다.
김형진 영재사관학원·수학영재만들기 대표 원장
1. 장로의 거짓말
한 종교인이 이와 같은 문제로 심각하게 고민하고 있었습니다.
그는 이 문제의 해답을 얻고자 여행을 떠났습니다. 여행 끝에 깊은 산 속의 수도원에서 수행하며 어떤 때는 참말만, 어떤 때는 거짓말만 하는 두 사람의 장로가 답을 알고 있다는 말을 듣고 수도원을 찾아가 장로를 만났습니다.
이 장로들에게 그가 고민하고 있는 문제의 해답을 물었을 때, 첫째 장로는 “나는 거짓말만 하지만 그 질문의 해답은 모른다네”라고 했고, 둘째 장로는 “나는 참말만 하지만 그 질문의 해답은 모른다네”라고 했습니다.
두 장로 중에 그 질문의 대답을 아는 사람이 있다는 것을 알고 있었으므로, 대답을 알고 있는 장로에게 “사후 세계는 없다네”라는 답을 들었습니다. 답을 알고 있는 장로는 누구이며 올바른 답은 어떤 것입니까?
√ 선생님의 도움
① 계획: 두 명의 장로가 참말을 하는 경우와 거짓말을 하는 경우로 나누어 생각해 봅니다.
② 실행:
1) 두 장로 모두 참말을 했다고 가정하면 첫째 장로는 자기 자신을 거짓말쟁이라고 했으므로 가정에 모순이 되고, 둘째 장로는 그 답을 모른다고 했으므로 답을 얻을 수 없습니다.
2) 첫째 장로는 참말을 하고, 둘째 장로는 거짓말을 했다고 가정하면 첫째 장로는 자기 자신을 거짓말쟁이라고 했으므로 가정에 모순이 되고, 거짓말을 한 둘째 장로가 한 말에서 참말만 한다는 말이 거짓말이고, 질문의 해답을 모른다는 말도 거짓말이므로 해답을 아는 것입니다.
3) 첫째 장로는 거짓말을 하고, 둘째 장로는 참말을 했다고 가정하면 첫째 장로는 자기가 거짓말쟁이라고 했으니 가정에 모순이고, 둘째 장로는 그 답을 모른다고 했으므로 답을 얻을 수 없습니다.
4) 두 장로 모두 거짓말을 했다고 가정하면 첫째 장로는 자기가 거짓말쟁이라고 했으니 참말을 한 것이 되어 가정에 모순이고, 둘째 장로는 거짓말만 하므로 그 질문의 해답을 모른다고 했으므로 해답을 아는 것입니다. 종교인이 둘째 장로에게 들은 해답이 ‘사후 세계는 없다네’이고, 거짓말만 하므로 올바른 답은 ‘사후 세계는 있다’는 것입니다.
③ 반성: 풀이 과정 중에 모순이 되는 부분이 있는지를 확인합니다.
2. 예언자의 처형
“나는 내일 너를 처형할 것이다. 넌 예언을 잘 한다고 하니 내일까지 일어날 일에 대하여 무슨 예언이든지 한 가지만 예언해 보아라. 그 예언이 맞으면 너를 반드시 교수형에 처할 것이고, 예언이 틀릴 경우에는 너를 반드시 단두형에 처할 것이다.”
이래도 저래도 죽을 수밖에 없는 처지가 된 예언자는 묘한 예언을 하여 왕이 교수형으로도 단두형으로도 처형할 수 없게 되었다고 합니다. 이 예언자는 어떤 예언을 했습니까?
3. 죄수 석방
왕은 세 죄수의 눈을 가리고 검은 모자를 각각의 머리에 씌운 후에 가린 것을 벗겨 눈을 떠 보게 했습니다. 죄수들은 다른 사람의 머리에 씌워진 모자는 볼 수 있어도 자기가 쓴 모자는 볼 수가 없었습니다. 왕이 죄수들에게 다음과 같이 말했습니다.
“너희들의 머리에는 검은 모자나 흰 모자가 씌워져 있다. 누구든지 흰 모자 두 개가 보이는 사람이나 자기 머리 위의 모자 색을 아는 사람은 손을 들어보아라. 그 사람은 살려주겠다. 단, 모자의 색을 알아맞힐 때는 그 이유를 설명해야 한다.”
세 명의 죄수가 대답을 못하고 망설이고 있다가 A가 손을 들어 자신의 머리에는 검은 모자가 씌워졌다고 말했습니다. A는 어떻게 검은 모자임을 알게 되었습니까?
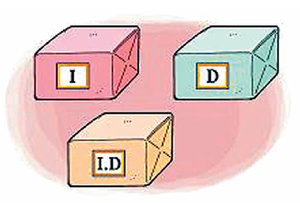
4. 스티커 정돈
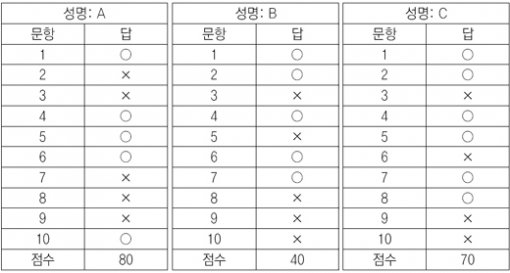
5. 정답지 만들기
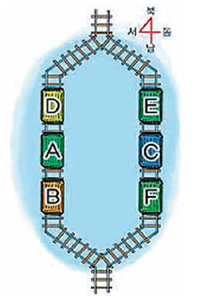
6. 여객차 연결
7. 3인조 도둑
[정답]
2=“나는 단두형에 처해질 것입니다.” 3=풀이 참조 4=풀이 참조 5=풀이 참조 6=풀이 참조 7=풀이 참조
▶easynonsul.com 및 수학영재만들기 홈페이지(tamnsu.com)에 풀이 및 동영상 강의
트렌드뉴스
-
1
오천피 시대 승자는 70대 이상 투자자…2030 수익률의 2배
-
2
김종혁 “친한계 탈당 없다…장동혁 체제 오래 못갈것”[정치를 부탁해]
-
3
배우 얼굴 가린다고…아기 폭우 맞히며 촬영, ‘학대’ 논란
-
4
트럼프 “대규모 함대 이란으로 이동 중…베네수 때보다 더 큰 규모”
-
5
“담배 끊으면 60만 원”… 보건소 맞춤형 금연 코칭
-
6
‘린과 이혼’ 이수, 강남 빌딩 대박…70억 시세 차익·159억 평가
-
7
“전기차 편의품목까지 다 갖춰… 신차 만들듯 고생해 만들어”
-
8
[단독]조여오는 25% 관세… “美 관보 게재 준비중”
-
9
화장실 두루마리 휴지는 ‘이 방향’이 맞는 이유
-
10
“코스피 5000? 대선 테마주냐” 비웃은 슈카, 조롱거리 됐다
-
1
李 “담배처럼 ‘설탕세’ 거둬 공공의료 투자…어떤가요”
-
2
국힘, 내일 한동훈 제명 속전속결 태세… 韓 “사이비 민주주의”
-
3
법원 “김건희, 청탁성 사치품으로 치장 급급” 징역 1년8개월
-
4
李 ‘설탕 부담금’ 논의 띄우자…식품업계 “저소득층 부담 더 커져”
-
5
장동혁 “한동훈에 충분한 시간 주어져…징계 절차 따라 진행”
-
6
李, 이해찬 前총리 빈소 찾아 눈시울… 국민훈장 무궁화장 직접 들고가 추서
-
7
“中여성 2명 머문뒤 객실 쑥대밭”…日호텔 ‘쓰레기 테러’ [e글e글]
-
8
‘김어준 처남’ 인태연, 소진공 신임 이사장 선임…5조 예산 집행
-
9
김종혁 “친한계 탈당 없다…장동혁 체제 오래 못갈것”[정치를 부탁해]
-
10
광주-전남 통합 명칭, ‘전남광주특별시’로 확정
트렌드뉴스
-
1
오천피 시대 승자는 70대 이상 투자자…2030 수익률의 2배
-
2
김종혁 “친한계 탈당 없다…장동혁 체제 오래 못갈것”[정치를 부탁해]
-
3
배우 얼굴 가린다고…아기 폭우 맞히며 촬영, ‘학대’ 논란
-
4
트럼프 “대규모 함대 이란으로 이동 중…베네수 때보다 더 큰 규모”
-
5
“담배 끊으면 60만 원”… 보건소 맞춤형 금연 코칭
-
6
‘린과 이혼’ 이수, 강남 빌딩 대박…70억 시세 차익·159억 평가
-
7
“전기차 편의품목까지 다 갖춰… 신차 만들듯 고생해 만들어”
-
8
[단독]조여오는 25% 관세… “美 관보 게재 준비중”
-
9
화장실 두루마리 휴지는 ‘이 방향’이 맞는 이유
-
10
“코스피 5000? 대선 테마주냐” 비웃은 슈카, 조롱거리 됐다
-
1
李 “담배처럼 ‘설탕세’ 거둬 공공의료 투자…어떤가요”
-
2
국힘, 내일 한동훈 제명 속전속결 태세… 韓 “사이비 민주주의”
-
3
법원 “김건희, 청탁성 사치품으로 치장 급급” 징역 1년8개월
-
4
李 ‘설탕 부담금’ 논의 띄우자…식품업계 “저소득층 부담 더 커져”
-
5
장동혁 “한동훈에 충분한 시간 주어져…징계 절차 따라 진행”
-
6
李, 이해찬 前총리 빈소 찾아 눈시울… 국민훈장 무궁화장 직접 들고가 추서
-
7
“中여성 2명 머문뒤 객실 쑥대밭”…日호텔 ‘쓰레기 테러’ [e글e글]
-
8
‘김어준 처남’ 인태연, 소진공 신임 이사장 선임…5조 예산 집행
-
9
김종혁 “친한계 탈당 없다…장동혁 체제 오래 못갈것”[정치를 부탁해]
-
10
광주-전남 통합 명칭, ‘전남광주특별시’로 확정
-
- 좋아요
- 0개
-
- 슬퍼요
- 0개
-
- 화나요
- 0개



댓글 0