[理知논술/중학생 통합교과 논술]⑫지구의 신비 밝히는 수리논술

‘과학적 분석+역사적 사실’

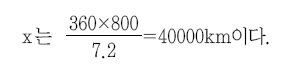
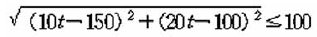
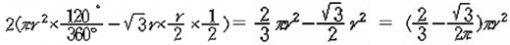
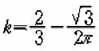
결합문제 출제 가능성 높아

지구와 우주의 불가사의한 신비로움은 고대부터 지금까지 일반 사람들을 비롯하여 여러 과학자의 호기심의 대상이었다. 지구가 구의 모양이라고 과학적으로 인식하기 전까지는 편평한 형태였다고 생각하였기 때문에 평면기하학에 따라서 지구를 분석하였고, 지동설이 받아들여지기 전까지는 천동설을 더 과학적인 것으로 생각하였다. 세월이 지나 더 과학적인 분석과 수리논리적인 사고가 발달함에 따라 지구와 우주에 대한 좀 더 논리적이고 사실적인 설명이 가능해졌다. 그럼에도 불구하고, 현재 태풍이나 지진과 같이 지구상에서 발생하는 자연재해에 대해서는 과학적인 방법을 사용하여도 정확한 예측이 불가능하다. 이뿐만 아니라 아직까지 지구의 많은 신비로운 현상은 논리적으로 설명할 길이 없어 새로운 방법의 수리 과학적이고 논리적인 분석과 연구가 필요하다.

따라서 다양한 수리논리적인 방식을 이용하여 접근할 수 있는 지구과학과 관련된 수리논술문제는 고대에서 현재에 이르기까지의 다양한 역사적 사실과 결합되어 출제될 가능성이 많다. 그러나 안타깝게도 다수의 문제가 고등학교 과정의 수학이론을 이용해야 하기 때문에 중학생 수준에서 해결할 수 있는 문제는 그렇게 많지 않은 것이 사실이다. 하지만 과학적이고 논리적인 분석을 통해 문제의 기본을 이해하는 능력과 더불어 고등학교 과정의 수학이론을 계속 습득하고 지구와 우주의 신비에 관련된 최근의 신문기사나 뉴스 보도에 주의를 기울인다면 어려운 수학이론을 사용하는 수리논술 문제도 고등학교과정을 이수한 후에 어렵지 않게 해결할 수 있으리라고 본다.

이번 호에서는 중학생들이 해결할 수 있는 지구의 신비와 관련된 수리논술 문제를 살펴보고, 문제를 정확히 이해하고 분석하여 이를 해결하는 방법을 알아보기로 한다.

[문제 1]

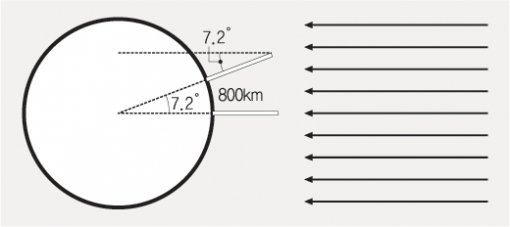
탈레스는 고대 그리스에서 피라미드의 높이를 직접 측정하지 않고 지팡이를 세워 지팡이와 피라미드 그림자의 길이 사이의 관계를 이용하여 피라미드 높이를 측정한 것으로 유명하다. 고대 그리스의 에라토스테네스는 이와 비슷하게 닮음을 이용해서 지구 둘레의 길이를 계산하였다. 그는 하짓날 정오에 시에네 지방에서는 햇빛이 우물 속 한가운데까지 수직으로 비치지만, 같은 시각에 시에네에서 북쪽으로 약 800km 떨어진 알렉산드리아에서는 그림과 같이 햇빛이 북쪽으로 약 7.2도 경사지게 비치고 있다는 사실을 발견하였다. 이를 기초로 태양광선이 평행하고, 지구가 완전히 구형이라고 가정한 후, 지구의 둘레를 구하라.

:풀이 해설 및 정답:

부채꼴의 호의 길이는 중심각의 크기에 비례하므로, 지구의 둘레를 xkm라고 하면, x : 800=360 : 7.2 이므로,

[문제 2]

동쪽으로 시속 10km로 항해하는 배가 있다. 이 배의 위치에서 동쪽으로 150km, 남쪽으로 100km 떨어진 해상에 중심이 있는 태풍은 시속 20km의 속도로 북쪽으로 진행하며, 그 중심에서 100km 이내에 폭풍우를 동반한다고 한다. 이 배가 이런 상황에서도 항해를 계속한다고 할 때, 폭풍우권 내에 최초로 들어가게 되는 것은 출발 후 몇 시간 후인가?

:풀이 해설 및 정답:

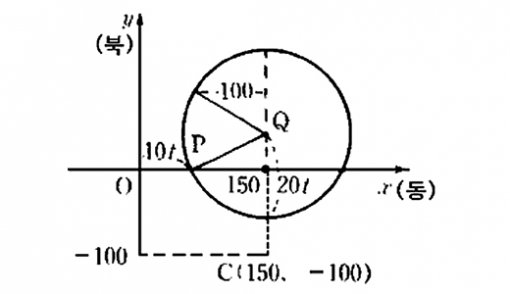
배의 현재 위치를 원점, 동쪽을 x축, 북쪽을 y축의 양의 방향으로 잡으면, 태풍 중심의 현재 위치 C는 C(150, -100), t시간 후의 배의 위치를 P, 태풍 중심의 위치를 Q라 하면 P(10t, 0), Q(150, 20t-100)가 된다.

배가 폭풍우권 내에 있을 조건은 PQ≤100 이므로

이고,

양변을 제곱하면 (10t―150)2+(20t―100)2≤10000가 된다.

이것을 정리하면 , t2―14t+45≤0, (t―5)(t―9)≤0에서 5≤t≤9

따라서 배는 최초로 5시간 후에 폭풍우권 내에 들어가서 5시간 후에 폭풍우권 내에서 벗어난다.

[문제 3]

개기일식이란 일식에서 태양이 달에 의해 완전히 가려지는 현상을 얘기한다. 황도와 백도의 교점은 황도상을 서쪽으로 움직이는데, 황도를 일주하는 데는 18.6년이 걸린다. 따라서 식의 계절은 매년 20일 정도 빠르게 일어난다. 태양이 백도와의 교점을 통과한 후 그 교점에 다시 돌아오는 데 걸리는 시간은 1항성년(恒星年:365일)보다 짧은 346.62일이다. 이것을 식년(蝕年)이라고 한다. 식의 계절은 1년에 두 번 일어나고 1식년 중에 일어나는 일식의 수는 2∼3회이다. 그중에는 개기일식과 금환일식은 일어나지 않을 때도 있고 1회 또는 2회 일어날 때도 있다. 1태양년 내에는 최고 5회, 최저 2회의 일식이 일어난다. 5회 일어나는 것은 극히 예외적인 일로서 1935년에 있었고 다음은 2206년에 있을 것이다.

진행 상황은 다음과 같다.

제1접촉: 태양의 서쪽에 어두운 달이 접근한다.

제2접촉: 태양이 달에 완전히 가려지고 정적이 깔리며 태양 주위에는 코로나가 보인다.

제3접촉: 서쪽으로부터 태양이 다시 나타나기 시작하는 때이다.

제4접촉: 하늘이 천천히 밝아지고 코로나가 보이지 않게 되며, 달은 태양으로부터 떨어진다

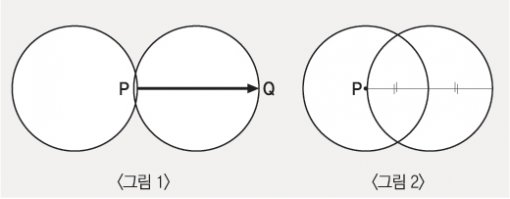
개기일식이 진행된 어느 날 제1접촉에서 제2접촉까지 1시간이 걸린다고 한다. 달과 해의 모양이 같은 크기의 원이라 가정하고 일식이 진행되기 시작하여 30분 후의 달과 해가 겹쳐진 부분의 넓이를 S′, 원의 넓이를 S라고 하면 S′=kS(단, k는 상수)이다.

이때 k 값을 구하여라.

:풀이 해설 및 정답:

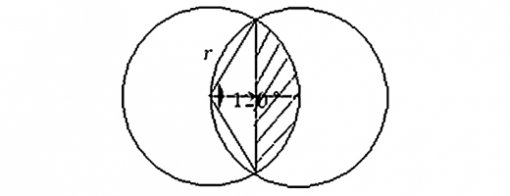
달이 P에서 Q까지 이동하는 데 1시간이 걸리므로 30분 후의 달과 해의 자취는 <그림 2>와 같다. 이때 겹쳐진 부분의 넓이는

중심각이 120°인 부채꼴의 넓이에서 꼭지각이 120°인 이등변 삼각형을 뺀 후 두 배하면 되므로 겹친 부분의 넓이를 구하는 식은 다음과 같다.

우리가 구하고자 하는 것은 S′=kS에서 k이고 S=πr2이므로

임을 알 수 있다.

심소연 정보학원 중등부 수학과 팀장