[理知논술/LEET의 A to Z]수리추리·논리게임 문제풀이

2009학년도 법학적성시험(LEET) 성적이 발표됨에 따라 이번 시험에서는 추리논증 과목이 언어이해 과목보다 어려웠다는 점이 객관적인 지표로 드러났다.

추리논증 과목에는 새로운 지문과 낯선 유형의 문제가 다수 출제되어 지원자들 사이에서 논란이 많았다. 하지만 논리학적 기초와 기본적인 수리 실력이 고득점의 핵심 역할을 했다는 점은 모의시험 때와 변함없었다.

LEET는 아직 완전히 정착하지 않은 시험이기 때문에 문제 유형과 난이도는 계속 진화할 것이다. 결국 LEET에 대비하기 위해서는 기본기를 갖추는 것이 가장 중요하다. LEET는 특정한 문제의 유형이나 그에 대한 해결책을 익히는 것보다 다양한 문제를 논리적으로 해결할 수 있는 사고의 훈련이 필요한 시험이다.

모의시험에 출제됐던 수리추리와 논리게임 문제를 풀며 추리논증 시험을 대비해보자.

○ 문제 1

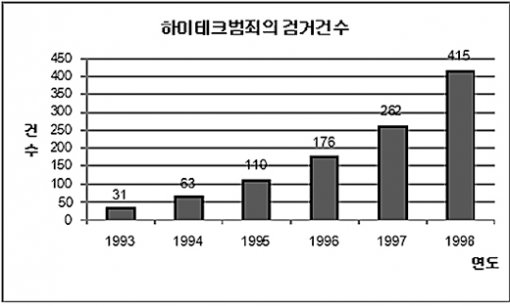
다음 그래프는 컴퓨터 기술이나 전기통신 기술을 악용한 하이테크범죄의 검거건수를 나타낸 것이다. 자료로부터 유추할 수 있는 내용으로 가장 적당한 것은?

br clear=all>

① 1994년부터 1998년에 걸쳐서, 검거건수의 전년도 대비 증가율이 가장 높은 것은 1994년이다.

② 1998년의 검거건수는 1993년의 15배이다.

③ 1993년부터 1998년에 걸쳐서 총검거건수는 1100건을 넘는다.

④ 컴퓨터의 보급 확대에 따라 하이테크범죄는 앞으로도 급속도로 증가할 것으로 예상된다.

⑤ 1995년부터 1998년까지의 모든 해에서 그 전 2년간의 검거건수 합계보다 많다는 것을 알 수 있다.

○ 풀이

전년도 대비 증가율을 비교할 경우 반드시 증가율 값 그 자체를 비교할 필요는 없다는 점에 주의해 문제를 풀어야 한다.

검거건수에 대해 전년도 값에 대한 당해연도 값의 비율을 비교하면 1994년은 이 비율이 2배를 넘는다. 하지만 1995∼1998년의 각 연도에서 2배를 넘는 해는 없다. 따라서 1994년의 전년도 대비 증가율이 가장 높다는 것을 알 수 있으므로 답은 ①번이다.

1993년의 검거건수는 31건이다. 여기에 15배를 하면 415건이 되므로 ②번은 오답이다. 1993∼1998년에서의 총검거건수를 모두 더하면 1057건이므로 ③번도 정답이 될 수 없다. ④번은 이 그래프만 보고 판단할 수 없는 내용이다. 1997년을 보면 그 전 2년간의 검거건수 합계가 286건으로 1997년보다도 많기 때문에 ⑤번도 답이 될 수 없다.

정답 ①

○ 문제 2

네 사람의 직업이 중복되지 않을 때 C의 직업은 무엇인가?

「① A가 목사라면 D는 배우이다.

② B가 은행원이라면 D는 의사이다.

③ C가 배우면 B는 은행원이다.

④ C가 의사가 아니라면 D는 목사다.

⑤ D가 의사가 아니면 B는 배우가 아니다.

⑥ B는 목사가 아니다.」

① 목사 ② 배우

③ 은행원 ④ 의사

⑤ 확정할 수는 없고 목사 또는 의사이다.

○ 풀이

D가 의사라면 ④에 의해 C는 의사가 되지만 그렇게 될 경우 C와 D 둘 다 의사가 되기 때문에 모순이 된다. 이를 통해 D는 의사가 아님을 알 수 있다. ②와 ⑤ 때문에 B는 은행원, 배우가 될 수 없다. ⑥을 통해서는 B가 목사가 아니라 의사라는 사실을 알 수 있다.

④에 의해 C는 의사가 아니므로 D는 목사라는 결론을 내릴 수 있다. 또한 ③에 의해 C는 배우가 아님을 알 수 있다. C는 의사도, 목사도, 배우도 아니므로 은행원이란 사실을 추론할 수 있다. 나머지 A는 배우가 될 수밖에 없다.

정답 ③

○ 문제 3

김 씨 부부는 파티를 열고 이 씨, 박 씨, 정 씨 세 쌍의 부부를 초대했다. 이들은 파티장에서 서로 악수를 했지만 자신의 배우자와는 악수를 하지 않았고 누구와도 두 번 이상 악수를 하지 않았다. 파티가 끝날 무렵 이들은 각자 악수를 한 횟수를 모두 다르게 말했다. 이 파티에서 김 씨 부인은 몇 번이나 악수를 했을까?

① 1번 ② 2번 ③ 3번

④ 4번 ⑤ 5번

○ 풀이

김 씨 부부를 Mr. K, Mrs. K, 이 씨 부부를 Mr. L, Mrs. L, 박 씨 부부를 Mr. P, Mrs. P, 정 씨 부부를 Mr. J, Mrs. J로 나타내기로 하자.

파티에 참석한 사람은 8명이고 자기 배우자와는 악수를 하지 않으므로 7번 이상 악수한 사람은 없다. 그러므로 악수한 횟수는 0, 1, 2, 3, 4, 5, 6 중 하나가 된다. 먼저 Mrs. K가 여섯 번 악수했다는 것은 자기 배우지 Mr. K를 제외한 모든 사람과 악수했다는 의미이므로 모순이다.

여섯 번 악수한 사람을 Mrs. K가 아닌 다른 사람이라고 가정해보자. 예를 들어 Mr. L이 여섯 번 악수를 했다면 Mrs. L의 악수 횟수는 0번이다. Mr. L이 자기 배우자를 제외한 김 씨 부부, 박 씨 부부, 정 씨 부부와 모두 악수했다면 이들은 모두 악수를 적어도 한 번은 하였으므로 악수 횟수가 0이 될 수 없다. 그러므로 0번 악수한 사람은 Mrs. L일 수밖에 없다.

이때 다섯 번 악수한 사람은 Mrs. K가 될 수 없다. Mrs. K가 다섯 번 악수했다면 Mr. K와 Mr. L을 제외한 나머지 모든 사람 Mr. P, Mr s. P, Mr. J, Mrs. J와 악수를 했어야 한다. 이들 네 사람 Mr. P, Mrs. P, Mr. J, Mrs. J는 Mrs. K와 Mr. L과 악수를 했으므로 적어도 두 번 이상 악수를 하게 된다. 이렇게 되면 한 번 악수한 사람이 없게 되므로 모순이 된다.

이제 다섯 번 악수한 사람을 Mrs. K가 아닌 Mr. P라 가정하자. 그러면 Mr. P는 Mrs. P와 Mrs. L을 제외한 다섯 사람, 즉 Mr. K, Mrs. K, Mr. J, Mrs. J, Mr. L과 악수를 한 것으로 볼 수 있다. 그런데 Mr. L은 Mr. K, Mrs. K, Mr. J, Mrs. J와도 악수했으므로 Mr. K, Mrs. K, Mr. J, Mrs. J는 적어도 두 번 악수를 한 것이 된다. 그러므로 악수를 한 번 한 사람은 Mrs. P이다.

또 네 번 악수한 사람은 Mrs. K가 될 수 없다. Mrs. K가 네 번 악수했다면 Mr. K, Mrs. L, Mrs. P를 제외한 네 사람과 악수한 것이 되기 때문이다. 이렇게 되면 Mr. J와 Mrs. J는 Mr. L, Mr. P, Mrs. K와도 각각 악수한 것이 되므로 이들은 적어도 세 번씩 악수한 것이 된다. 두 번 악수한 사람이 없다는 전제에 반하기 때문에 Mrs. K는 4번 악수할 수는 없다.

이제 네 번 악수한 사람을 Mr. J라고 가정하자. 그러면 Mrs. K는 Mr. L, Mr. P, Mr. J와 악수한 것이 되므로 두 번 악수한 사람은 반드시 Mrs. J가 되어야 한다. 마지막으로 세 번 악수한 사람이 Mrs. K가 된다.

결론적으로 김 씨 부부는 세 번씩, 이 씨 부부가 여섯 번과 0번, 박 씨 부부가 다섯 번과 한 번, 정 씨 부부가 네 번과 두 번씩 악수한 것이 된다.

정답 ③

○ 문제 4

종이 한 장에 1번부터 50번까지의 50개의 문장이 쓰여 있다. 모든 문장의 내용은 똑같지만 숫자만 달라진다.

「1. 이 종이에 쓰인 문장 중 꼭 1개가 거짓이다.

2. 이 종이에 쓰인 문장 중 꼭 2개가 거짓이다.

3. 이 종이에 쓰인 문장 중 꼭 3개가 거짓이다.

↓

50. 이 종이에 쓰인 문장 중 꼭 50개가 거짓이다.」

이 문장이 무수히 반복될 경우 마지막 문장은 ‘이 종이에 쓰인 문장 중 꼭 n개가 거짓이다’가 된다. 그렇다면 과연 어떤 문장이 참일까? 참인 문장의 개수(A)와 참인 문장의 번호(B)의 합을 구하라. 단, 참인 문장이 여러 개인 경우 B는 각 번호의 합으로 한다.

① 10 ② 20 ③ 50

④ 65 ⑤ 75

○ 풀이

만약 50개의 문장 중 2개 이상의 문장이 참이라면 그들 문장의 내용에서 정확히 n개의 문장이 참이라는 명제와 모순이 된다. 그러므로 많아야 한 문장만이 참이 될 수 있다. 만약 참인 문장이 하나도 없다면 50개의 문장이 모두 거짓이 된다. 이럴 경우 50번째 문장이 참이 되어 또 모순이 된다. 따라서 49개의 거짓인 문장이 있게 되어 49번째 문장이 참이다. 즉, A는 1이고 B는 49가 되므로 A와 B의 합은 50이다.

정답 ③

○ 문제 5

A∼D의 4개 도시가 있다. 어떤 사람이 차로 어느 도시를 출발해, 다른 도시에 한 번씩 들러 다시 처음의 도시로 돌아온다. 어떤 사람이 운전하는 차로 각 도시를 이동할 때의 연료 소비량이 표와 같을 경우, 최소가 되는 경우의 연료 소비량은 얼마인가.

br clear=all>

① 35L ② 36L ③ 37L

④ 38L ⑤ 39L

○ 풀이

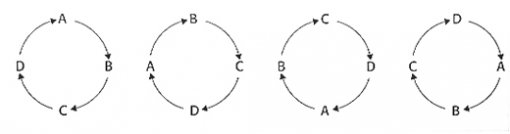
아래의 그림 4개는 모두 같은 방법으로 회전한다. 회전할 때 동일해지는 순회 방법이 나오지 않도록 1개를 고정해서 생각하면(원순열) 전부 6가지를 적을 수 있다.

br clear=all>

A-D-C-B-A순으로 돌 때 36L로 연료 소비량이 가장 적으므로 정답은 ②번이다.

정답 ②

육轢