[신나는 공부]창의력을 잡아주는 해법수학교실/최적경로 설계

《경로 설계의 밑바탕이 되는 ‘한 붓 그리기’는 영재교육원 입시 문제로 자주 출제됩니다. 특히 최근에는 한 붓 그리기를 실생활과 연관시킨 ‘최적경로 설계’ 문제가 자주 등장하고 있습니다. 경로설계 유형의 문제는 어떻게 해결해야 하는지 알아보도록 하겠습니다.》

● 문제 1

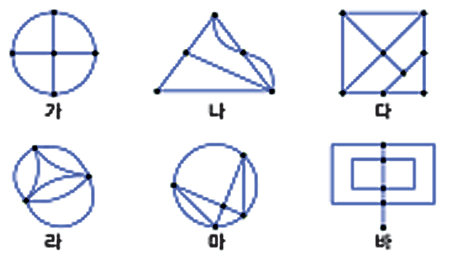
점과 선으로 이루어진 도형들이 오른쪽 그림과 같이 여섯 개 있습니다. 물음에 답하시오.

⑴ 홀수 개의 선이 연결된 점을 홀수점, 짝수 개의 선이 연결된 점을 짝수점이라고 합니다. 홀수점이 두 개 있는 도형은 두 개의 홀수점이 각각 출발점과 도착점이 되어야 합니다. 왜 그런지 이유를 설명하시오.

⑵ 한 점에서 시작해 모든 선을 한 번씩만 지난 다음 출발점으로 돌아올 수 있는 도형을 찾아 쓰시오.

● 문제 2

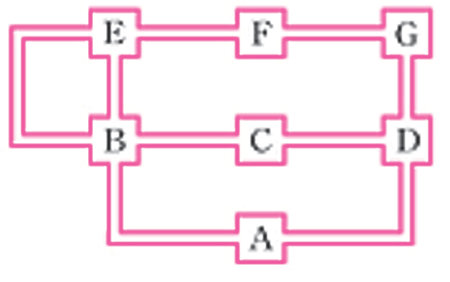
오른쪽 그림과 같이 어떤 성에 방이 7개 있습니다. 방들 사이는 복도로 연결돼 있습니다. 입구로 들어가서 모든 복도를 한 번씩만 통과한 다음 출구로 나가려면 입구와 출구를 각각 어떤 방에 만들어야 합니까? (가능한 경우를 모두 쓰시오.)

【생각의 흐름】

① 각 방을 점으로, 복도를 선으로 생각하고 홀수 개의 선이 연결돼 있는 점을 찾아봅니다.

② 어떤 경우에 모든 복도를 한 번씩만 통과하게 되는지 알아봅니다.

③ 홀수점에 해당하는 방에 출구와 입구를 만들면 됩니다.

● 문제 3

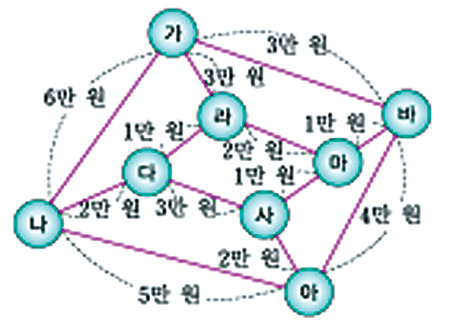
오른쪽 그림에서 원은 도시, 선은 도로를 나타냅니다. 선에 쓰인 숫자는 도로를 지날 때 내야 하는 통행료를 의미합니다. (가) 도시에서 출발해 모든 도시를 거친 다음 다시 (가) 도시로 돌아오려면 최소한 얼마의 통행료를 준비해야 합니까?

☞ Step 3 문제의 정답을 엽서로 보내 주시는 학생 중 매주 10명을 선정하여 3만 원 상당의 문화상품권을 드립니다.

(자세한 내용은 홈페이지 참조)

○ 정답 및 해설 보기: ㈜천재문화/해법수학교실 홈페이지(www.hbmath.co.kr)

○ 엽서 보내실 곳: 서울 금천구 가산디지탈 1길 217 ㈜천재문화 홍보기획팀