[理知논술]논술에 강한 수학

1/3/4/2/2/3/4

심판 7명이 매긴 제각각 순위

이 선수가 받을 최종 등수는?

지난 시간에는 몇 가지 기초적인 등위 결정법에 대해 알아봤다. 이번 시간에는 복잡하지만 좀 더 합리적인 등위 결정법을 알아보자.

○ 보편적인 등위 결정 방법

심판이 선수들의 순위를 결정하면, 각 선수의 등위를 심판들의 투표에서 다수결에 따라 결정하는 방법이다. 다음 예를 통해 알아보자. 두 명의 선수 A, B가 7명의 심판으로부터 다음과 같은 순위를 받았다.

A : 3 / 3 / 4 / 3 / 3 / 2

B : 4 / 3 / 3 / 4 / 3 / 3

A선수의 경우 다수결에 따라 2위일 가능성은 없다. 따라서 A선수가 받은 순위 중에서 2위인 것을 3위라고 생각하면 A는 5명의 심판으로부터 3위, B는 4명의 심판으로부터 3위를 받았으므로 A가 3위, B가 4위이다.

이런 방법을 좀 더 체계적으로 쓰면 다음과 같다.

1- 과반수의 심판이 매긴 순위를 ‘결정된 등위(deciding place=DP)’라고 한다.

2- k등과 k등보다 더 높은 순위를 받은 선수가 k등이 된다.

A : 1 / 2 / 1 / 3 / 1 / 2 / 1

B : 1 / 3 / 4 / 2 / 2 / 3 / 4

위의 규칙을 가지고 A, B의 순위를 매겨 보자. A는 1위가 된다. 왜냐하면 1위를 과반수의 심판으로부터 받았기 때문이다. 반면에 B는 몇 위인가? 1위를 1명으로부터 받았다. 2위는 2명이므로 2위 이상의 순위는 3명의 심판으로부터 받았다. 아직 과반수에 도달하지 못했으므로 3위까지의 심판 수를 세면 5명이므로 3위인 것이다.

이제 순위를 쉽게 결정할 수 없는 경우에 어떻게 하는지 살펴보자.

방법 1. 위의 방법으로 결정된 등위가 같은 두 선수가 있을 때는 어떻게 판단하는가? 다음 예를 보자.

A : 1 / 2 / 4 / 3 / 3

B : 2 / 1 / 4 / 4 / 3

두 선수의 DP는 모두 3위다. 이럴 때는 ‘등위 결정의 수(number of deciding places=NDP)’를 고려한다. 두 명 이상의 선수의 DP가 같을 때는 NDP가 높은 선수가 높은 등수를 받는다. 즉 예에서 선수 A의 NDP는 3위 이상으로 판단한 심판의 수로 4가 된다. 반면 선수 B의 NDP는 3이므로 A가 3위, B가 4위다.

방법 2. 하지만 다음의 예를 보자.

A : 1 / 2 / 3 / 4 / 3

B : 1 / 3 / 1 / 3 / 5

선수 A와 B의 DP는 모두 3이고 NDP는 4로 동일하다. 이럴 때는 ‘결정된 등위의 수의 합(sum of deciding placse=SDP)’과 ‘등위의 합(sum of places=SP)’을 고려한다. 선수 A의 SDP는 9(3위 이상으로 판단한 심판들의 결정했던 순위들의 합, 1+2+3+3)이고 B의 SDP는 8(1+3+1+3)이다. 즉, 선수 B의 SDP가 선수 A보다 작으므로 B선수가 3위, 선수 A가 4위이다.

그렇다면 이런 경우에는 어떻게 해야 할까?

A : 1 / 1 / 2 / 2 / 3

B : 1 / 1 / 2 / 2 / 4

두 선수의 DP, NDP, SDP가 모두 동일하다. 이럴 때는 SP를 비교한다. 즉 모든 심판들이 결정했던 순위의 합을 비교하는 것이다. 선수 A의 SP는 9, 선수 B의 SP는 10이므로 SP가 작은 선수 A가 2위, 선수 B가 3위다.

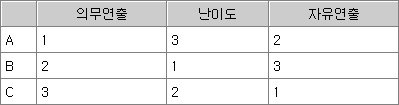
방법 2. A, B, C 세 선수가 한 심판으로부터 세 분야에 대해 다음과 같은 평점을 받았다.

이 경우에는 앞의 어떤 방법으로도 등위를 결정할 수가 없다. 이럴 때는 평가항목에 가중치를 두어 등위를 결정하게 된다. 예를 들어 의무 연출 부문에는 0.5, 난이도에는 0.3, 자유연출에는 0.8의 가중치를 두게 된다면 B가 1위, A가 2위, C가 3위이다.

A : 1×0.5+3×0.3+2×0.8=3

B : 2×0.5+1×0.3+3×0.8=3.7

C : 3×0.5+2×0.3+1×0.8=2.9

등위 결정법은 많은 발전을 거쳐 왔다. 기록이 아닌 내용을 심판들이 평가하여 순위를 정할 때 일어날 수 있는 논란을 없애기 위해 꾸준히 수정되어 온 것이다. 그 발전에는 항상 수학적 밑바탕이 깔려 있었다.

안성환 ㈜엘림에듀 집필위원