[理知논술]대입논술, 이것만은 알아두자

■ 자연계 학생 논리적 글쓰기

‘p이면 q’ 논증, p가 참인지 꼼꼼히 따지자

[논제] 줄무늬 하이에나는 외관상 친밀감을 주는 동물이 아니며 인간에게 유용한 어떤 것을 제공하지도 않는다. 그런데도 유엔 산하 국제기관은 이 동물의 멸종을 막기 위해 노력하고 있다. 줄무늬 하이에나의 멸종을 막기 위해 우리가 계속 노력해야 하는 이유에 관하여 논하라.

[학생 답안]

주변에서 많은 생물들을 발견할 수 있다. 가령 서울 도심에 가까운 난지도에서도 수백 종의 동물이 살고 있다. ①이 많은 생물들은 서로 먹고 먹히는 관계를 통해 하나의 생태계를 이룬다. ②특히 먹이사슬은 생물들의 개체 수를 조절하는 중요한 요인이기 때문에, ③먹이사슬의 안정성이 파괴되면 결국 전체 생태계가 위협 받을 수 있다. ④가령 줄무늬 하이에나가 멸종한다면 그 먹이가 되는 동물은 포식자가 없어진 틈을 타 무한증식하게 될 것이다. ⑤그런데 실제로도 줄무늬 하이에나가 최근 멸종 위기에 처해 있다고 한다. ⑥따라서 줄무늬 하이에나의 먹이가 되는 동물이 증식하면서부터 서식처나 먹이를 공유하는 여러 다른 생물종의 생존이 크게 위협받게 될 것이다. ⑦한편 피식자와 포식자의 경쟁적 관계는 상호작용을 통해 서로의 진화를 유도한다고 한다. ⑧물론 생물들은 진화를 통해 환경에 대한 적응력을 끊임없이 키워왔다. ⑨따라서 안정된 먹이사슬은 생물들의 환경 적응력을 높이는 데 매우 중요하다는 사실을 알 수 있다. ⑩그러므로 여러 생물종의 고사나 멸종은 그보다 더 많은 생물종으로 하여금 환경 변화에 적절히 대응하지 못하게 함으로써 결국 생태계 전체가 동반멸종의 길에 들어설 것이다. ⑪인류는 이러한 파국을 막아야 할 이유를 알고 있으며 파국의 원인에 대하여 책임이 있다. 따라서 줄무늬 하이에나는 보존되어야 한다.

[논증 분석]

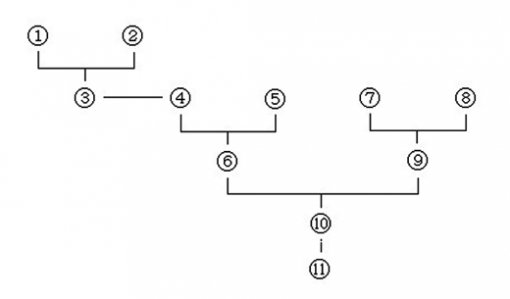
위 글은 아래 그림(‘논증나무’라고 부름)과 같은 논증 구조를 갖고 있다. 논리성 면에서는 만점을 줄 만한 글이다. 물론 학생이 쓴 글이라는 전제에서 말이다. 평균적인 학생들은 논증나무에서 기둥이 오직 한 번 분기하는 방식으로 글을 쓴다. 심지어 분기되어 나타난 가지들 간에 논리적 연관성이 없는 경우도 허다하다. 그러나 위 글은 그러한 문제를 모두 극복하고 다채로우면서도 치밀한 논증의 형태를 보여준다.

[평가]

논증은 좁은 의미에서 보면 자신의 주장을 방어하는 것이고, 넓은 의미에서 보면 다른 사회적 주체를 설득하는 것이다. 따라서 논증을 평가하는 기준은 ‘논증의 타당성’과 전제들의 진리 여부를 확인하는 ‘논증의 건전성’이어야 한다. 여기에서는 논증의 타당성을 검토해보기로 한다. 그렇다면 위 글은 타당한가? 답은 연역적으로나 귀납적으로 타당하지 못하다는 것이다. 이제부터 위 글의 문제가 무엇인지 알아보자.

위 글의 요지는 ‘생태계의 파국을 막기 위해 하이에나를 지켜야 한다’ 혹은 ‘생태계의 파국을 막기 위해 종의 보존에 힘써야 한다’이다. 비록 주장 자체는 모두를 위해 좋은 내용을 담고 있지만, 충분히 타당한 논증은 아니다. 타당성을 훼손하는 원인은 문장①, ②, ③에 있다. 특히 문장③의 ‘먹이사슬의 안정성이 파괴되면 결국 전체 생태계가 위협받을 수 있다’는 말은 종의 구성비가 크게 변하면 많은 종들이 멸종할 수 있다는 의미로 해석해야 하는데, 실제로 그런 일이 벌어질 가능성은 매우 낮다. 자연적인 원인으로도 종의 구성비는 종종 크게 변해왔으며, 그런 혼란 상태의 생태계라 할지라도 대부분 정상적으로 복원되어 왔으리라고 추정되기 때문이다.

위 글에 쓰인 많은 논증이 ‘p이면 q이다’와 같은 전제를 갖지 않고 ‘대부분의 p는 q이다’ 혹은 ‘p의 75%는 q이다’라는 전제를 갖고 있다. 이유가 무엇이든 이런 논증은 연역적으로 타당할 수 없다. 만약 유일하게 제시된 전제 p가 실제로 q를 이끌어낼 개연성이 상당히 높았다면 귀납적으로는 합당한 글이 됐을 것이다. 그러나 위 글의 경우, 전제 p(먹이사슬의 안정성이 파괴되면)가 q(결국 전체 생태계가 위협받을 수 있다)를 이끌어낼 가능성이 매우 낮기 때문에 귀납적으로도 합당한 글이 아니다.

만약 전제 p가 q를 이끌어낼 가능성이 높으면 p를 전제로서 사용할 수 있을 것이다. 즉, 참일 가능성이 거짓일 가능성보다 높은 전제를 사용할 경우 결론이 틀렸다고 볼 수 없다는 뜻이다.

■ 과학, 논술을 만나다

이런기체 저런기체 종류는 다양한데…

기체상수의 크기는 왜 똑같을까