[理知논술]초등 생각하는 수학

입력 2006년 6월 20일 03시 01분

교육청 영재교육원은 초등 3학년부터 선발한다. 영재교육원의 수료자는 다른 영재교육원에 지원할 때 학교장 추천과 상관없이 별도의 지원자격을 얻는다. 평소 심화문제로 공부했기 때문에 어려운 선발 시험에서 유리하다. 따라서 초등 3학년 이후 영재교육원에 입학하기는 사실상 어렵다. 영재교육원을 염두에 두고 있는 학생이라면 초등 3학년 때 입학한다는 각오로 일찍 준비하는 것이 좋다.

단순계산력 위주의 학습으로는 영재교육원 시험을 대비할 수 없고, 통합사고력 위주의 학습이 필요하다. 통합사고력 학습은 단시일 내에 완성할 수 없기 때문에 최소 초등 1학년, 이르면 유아단계에서부터 이런 학습을 할 필요가 있다. 또한 초등 1학년 또는 유아의 경우 1, 2년의 선행학습이 필요하다. 선행학습은 개념을 위주로 해 차츰 사고력 학습으로 옮겨가는 것이 좋다.

논리 사고력 학습의 경우, 1차 논리사고 검사와 2차 창의적 문제해결력 검사에서 도형, 카드 등을 활용한 문제가 출제된다. 평소 수학 교구재 등을 활용해 다양한 조건 속에서 다양한 활용을 통해 사고력을 키워야 한다.

또한 다양한 형태의 배열 속에서 규칙성을 찾는 문제와 문장제 형태의 문제들을 풀어보는 것도 사고력 학습에 도움이 된다.

심화문제의 경우 경시대회 문제와 같이 수학에 바탕을 둔 통합사고력 문제, 특히 문장제 형태의 문제와 서술형태의 문제를 준비하는 것이 바람직하다. 2차 창의적 문제해결력 검사는 대부분 단답형 주관식과 서술형 혼합형으로 출제된다. 특히 2교시의 경우 5문제 모두 서술형으로 출제된다.

실전경험을 쌓기 위해 경시대회에 출전해보는 것도 많은 도움이 된다. 경시대회에 출전해 본인의 위치를 점검함과 동시에 실전경험을 쌓을 수 있다. 경시대회는 단답형 주관식과 서술형태로 출제되는 한국수학인증시험(KMC)과 한국수학올림피아드(KMO) 등이 좋다.

마지막으로 영재교육원에서 이뤄지는 수업내용을 학습하는 것도 도움이 된다. 각 영재교육원 홈페이지를 방문하면 학습내용 또는 과제가 공개돼 있다.

임성호 ㈜하늘교육 기획실장

▼ 규칙성과 함수 ▼

1. 영희가 성냥개비로 다음과 같은 모양을 만들고 있습니다. 영희가 100개의 성냥개비를 가지고 있을 때, 가장 큰 모양을 만들고 남은 성냥개비는 몇 개일까요? (단, 작은 정사각형의 한 변은 성냥개비 1개로 만든 것입니다.)

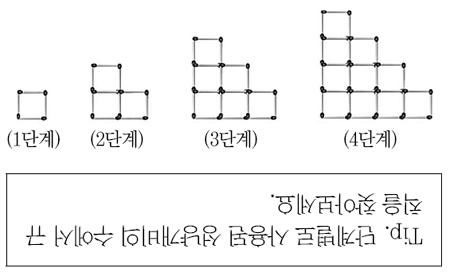2. 자연수를 다음 표와 같이 배열할 때, 200번째 줄의 넷째 자리에 위치하는 수는 얼마인가요?

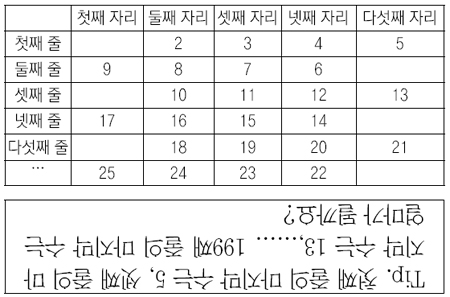▼ 수와 연산 ▼

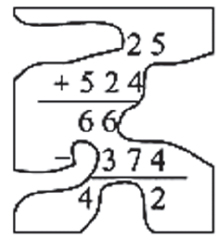1. 다음은 네 자리 자연수의 덧셈과 뺄셈을 계산한 종이의 일부가 찢긴 그림입니다. 보이지 않는 숫자를 찾아 모두 더하면 얼마인가요?

2. 어떤 자연수로 1186을 나누면 1이 남고, 1661을 나누면 2가 남으며, 2209를 나누면 3이 부족하다고 합니다. 이런 수 중 가장 큰 수는 얼마인가요?

3. 어느 서점에 사람들이 책을 사려고 줄을 서 있습니다. 앞에서부터 차례로 1, 2, 3…의 번호표가 주어졌습니다. 앞에서부터 15명이 책을 사고 돌아갔고, 남은 사람들 중에 나를 제외한 사람들의 번호의 합이 나의 번호보다 494가 더 크다면 나의 번호는 얼마인가요?

▼ 도형 ▼

1. 아래 그림에서 전체의 5분의 2만큼 색칠을 하려고 합니다. 가장 작은 삼각형 몇 개에 색칠을 해야 할까요? (작은 삼각형의 크기는 모두 같습니다.)

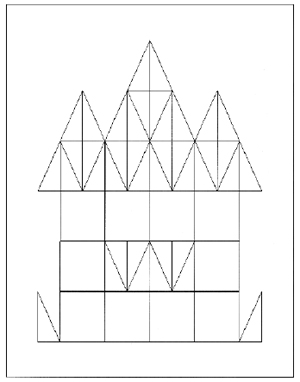① 28개 ② 30개 ③ 32개 ④ 34개 ⑤ 36개

2. 평행사변형 ㄱㄴㄷㄹ에서 선분 ㅁㅂ은 대각선 ㄱㄷ과 평행합니다. 아래의 그림에서 삼각형 ㄱㅁㄹ과 넓이가 같은 삼각형은 모두 몇 개인가요?

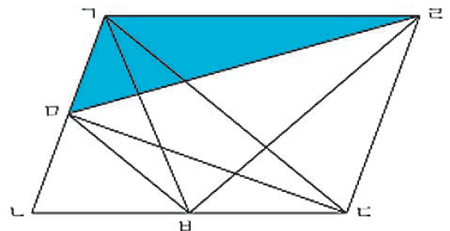① 1개 ② 2개 ③ 3개 ④ 4개 ⑤ 5개

3. 색종이를 아래 그림과 같이 두 번 접었습니다. 이렇게 접힌 색종이를 가로와 세로로 점선을 따라 가위로 두 번 자르면 모두 몇 조각이 될까요?

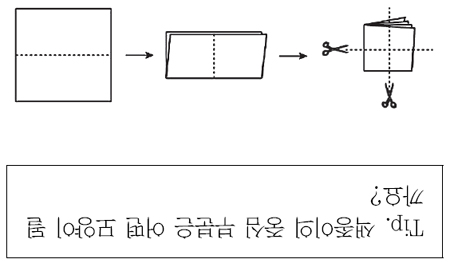▼ 측정 ▼

1. 작은 정육면체 27개를 면끼리 붙여서 큰 정육면체를 만든 후에, 아래 그림과 같이 굵은 선을 따라 잘랐습니다. 이때, 잘린 두 부분 중 색칠된 부분의 크기는 작은 정육면체 몇 개의 크기와 같을까요?

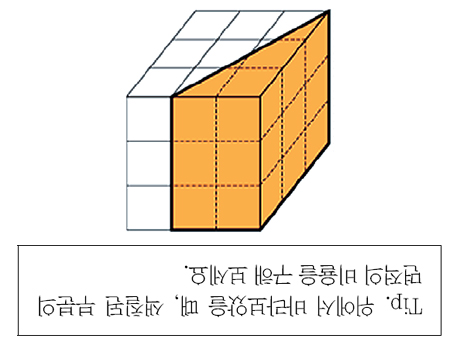2. 다음 그림은 크기가 같은 원 14개를 서로 맞닿게 늘어놓은 것입니다. 굵은 선 부분의 길이가 168cm라면 원의 반지름은 몇 cm인가요?

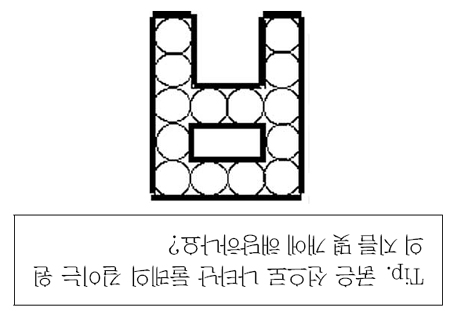3. 오른쪽 그림은 1800년경 프랑스에서 쓰였던 10진법의 시계입니다. 이 시계는 하루에 짧은 바늘이 한 바퀴, 긴 바늘이 열 바퀴 돕니다. 오른쪽 그림과 같이, 짧은 바늘이 3과 4 사이에 있고 긴 바늘이 5를 가리킬 때, 요즘의 시간으로 오전 몇 시 몇 분인지 구하세요. (단, 짧은 바늘과 긴 바늘이 모두 10을 가리킬 때, 요즘 시간으로 자정을 나타냅니다.)

4. 오른쪽 그림에서 가장 바깥쪽 원의 지름은 12cm이고, 원 안에 있는 사각형은 모두 정사각형입니다. 작은 정사각형 안의 색칠된 삼각형이 이등변삼각형일 때, 이 이등변삼각형의 넓이는 얼마입니까?

① 18cm² ② 36cm² ③ 72cm²

④ 90cm² ⑤ 144cm²

▼ 문자와 식 ▼

1. 다음 <보기>의 숫자들과 같은 규칙으로 오른쪽 그림을 만들었습니다. 같은 기호는 같은 수를 나타낼 때, ●에 들어갈 수는 얼마인가요?

2. 다음 10개의 ○ 안에 1부터 10까지의 자연수를 한 번씩만 써 넣어 큰 원 위에 있는 6개 숫자의 합이 모두 36이 되도록 할 때, ‘가+나’의 값은 얼마인가요?

3. (가)와 (나) 두 어린이가 어떤 게임을 하는데, 이긴 사람이 4점, 진 사람이 2점의 점수를 받기로 하였습니다. 두 어린이가 게임을 20번 한 후 서로 얻은 점수를 비교해보니 12점의 점수 차이가 났습니다. 점수가 낮은 어린이가 얻은 점수는 몇 점일까요?

4. 무게가 201g, 299g, 400g, 600g, 900g인 사과가 1개씩 놓여 있는 책상을 향해 두 사람이 동시에 달려가서 도착한 순서대로 사과를 1개씩 선택한 다음, 두 사람이 동시에 사과를 먹기 시작했습니다. 책상에 먼저 도착한 사람이 항상 더 많은 양의 사과를 먹으려면, 처음에 몇 g짜리 사과를 선택해야 할까요? (단, 두 사람이 g당 사과를 먹는 빠르기는 같으며, 한 번에 1개씩만 먹습니다.)