재미있는 ‘수학적 모델링’
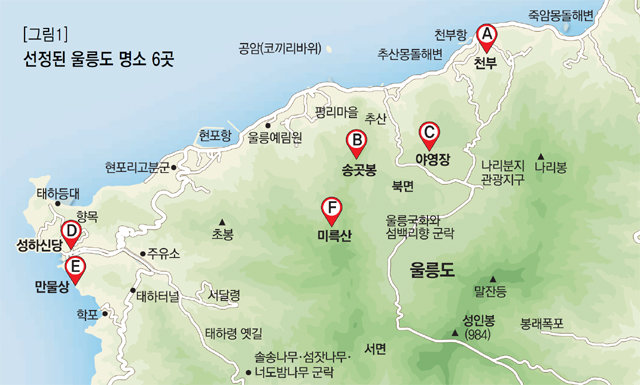
여름휴가철과 맞물려 전국에 가마솥더위가 기승을 부리면서 해외로 떠나는 사람도 크게 늘 것으로 보입니다. 서영도 더위를 피해 시원한 곳으로 가족 여행을 가자고 제안합니다.
서영: 엄마. 이번 여름에는 더위를 식힐 겸 좀 새롭고 다양한 볼거리가 있는 곳으로 가족여행을 가면 어떨까요?
엄마: 그래. 그런 곳으로 가면 좋겠구나.
엄마: 미리 준비가 필요한데 말이야. 그럴 때 수학이 여행을 좀 더 매력적으로 만들어 줄 수도 있단다.
○ 수학적 모델링으로 여행 계획을 짜자
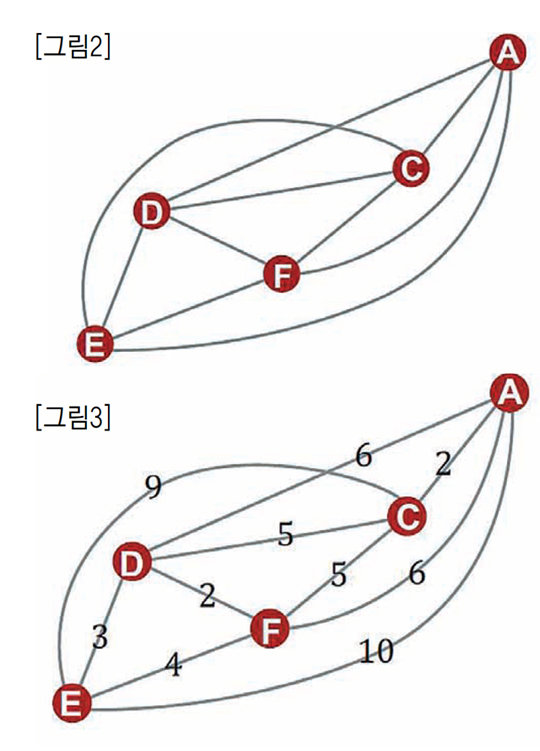
이때 여러분이 선택한 출발 지점에서 여행을 시작해 한 번씩만 선택한 장소를 다닌 후 다시 출발 지점으로 돌아오는 방법이 얼마나 많이 있을지 생각해 보세요. 어떤 방법이 있을까요? 수학자가 경로를 표시하는 한 가지 방법은 ‘그래프’를 사용하는 것입니다. 여기서 그래프는 우리가 흔히 이야기하는 함수의 그래프가 아닙니다. 관심 있는 지점을 점으로 표현하고 이때 어느 두 점을 선으로 연결하여 나타낸 것을 말합니다. 표시한 점을 ‘꼭짓점’, 연결한 선을 ‘변’이라고 부르지요. 우리가 선택한 여행지를 그래프로 연결하면 [그림2]와 같습니다.
여러분은 어떤 모델을 사용했나요? 위와 같은 모델은 가능한 여러 경로를 확인하는 데 도움이 되지만 최고로 좋은 관광 경로를 선택하는 데 있어서는 모든 경우를 구해봐야 하는 한계가 있습니다.
여기서 잠깐! 모든 지점을 지나는 가능한 경로는 모두 몇 가지나 될까요? 처음 시작할 지점이 5가지, 그 다음 방문할 수 있는 곳이 4가지…. 이렇게 생각해보면 5×4×3×2×1=120가지 인 것을 알 수 있습니다.
최고의 경로를 위해 그래프를 그리는 데 고려하지 않은 요인이 있는지 살펴보고 반드시 생각해야 할 요소가 있다면 첨가해서 수정합니다. 제한된 시간에 움직이려면 최소한의 시간이 중요한 요소가 될 수 있습니다. 따라서 각 지점 간의 이동거리가 중요하겠지요. 각 꼭짓점 간의 이동시간(분)을 예를 들어 표시한 그래프는 [그림3]과 같습니다.
○ 해밀턴 경로로 최적의 경로를 찾자
최고로 좋은 관광 경로를 찾으려고 120개나 되는 경로를 다 생각해볼 수는 없겠죠. 한 꼭짓점에서 시작하여 그래프의 각 꼭짓점을 정확히 한 번씩 방문하여 다시 원래 꼭짓점으로 돌아오는 경로를 ‘해밀턴 경로’라고 합니다, 효율적인 해밀턴 경로를 찾는 데 도움이 되는 몇 가지 조건이 있습니다.
①두 꼭짓점 사이를 이동하는 비용은 어느 방향으로나 같다. 즉, 비용은 대칭이다.
②꼭짓점 A에서 꼭짓점 B로 가는 비용은 꼭짓점 A에서 꼭짓점 C를 거쳐 꼭짓점 B로 가는 비용보다 작거나 같다.
③각 꼭짓점은 모든 다른 꼭짓점에 변으로 연결된다. 즉, 두 점은 모두 변으로 연결되어 있고 이를 완전그래프라고 한다.
‘그림4’는 조건 ①, ③은 만족하지만 A-E=10인데 A-D+D-E=9로 ②를 충족시키지 않는 것으로 보입니다. 그러나 이는 시간을 반올림하는 과정에서 일어난 일로 10으로 바꾸어 생각해도 되기에 조건을 만족한다고 봅니다.
최적의 경로를 정하기 위해 꼭짓점 A부터 시작해봅시다. C는 A에 가장 가깝기 때문에 경로 A-C-A를 생각해봅시다. 그럼 D와 F는 경로 A-C-A에 가장 가까우면서 이 경로에는 없는 꼭짓점입니다. 따라서 F를 선택하면 경로 A-F-C-A가 됩니다. 또 이 경로에 없지만 가장 가까운 꼭짓점 D를 생각하면 경로 A-D-F-C-A를 구할 수 있습니다. E는 D와 3만큼 거리이므로 D 앞으로 순서를 정합니다. 그럼 총 소요시간이 22인 거의 최소 경로를 얻을 수 있습니다.
다른 꼭짓점을 시작점으로 하여 다시 비슷한 방식을 적용합니다. C를 시작점으로 사용하면 총 소요시간이 20인 경로 C-A-F-E-D-C를 구할 수 있습니다. D로 시작하면 총 소요시간인 23인 경로 D-F-E-A-C-D를 구할 수 있습니다. E로 시작하면 총 소요시간이 22인 경로 E-A-C-F-D-E를 찾을 수 있습니다. 따라서 가장 좋은 결과는 20입니다.
○ 수학적 지식 실생활에 적용 능력 필요
이제 수학적으로 해결한 결과를 판단하고 실생활에 적용할 차례입니다. 결국 우리가 계획할 수 있는 최고의 경로는 야영장에서 출발해 천부, 미륵산, 만물상, 성하신당 순으로 이동하여 야영장으로 돌아오는 경로가 됩니다.
어떤가요. 수학적 모델링의 위력을 느끼셨나요? 현재와 앞으로는 수학적 지식보다 그 지식을 이렇게 실생활에 적용하는 능력이 더 중요한 시대랍니다. 더위를 피해 또는 휴식을 위해 여행을 계획하는 이때 수학과 함께 여행을 계획해 보세요.
박지현 반포고 교사
-
- 좋아요
- 0개
-
- 슬퍼요
- 1개
-
- 화나요
- 0개



댓글 0