[理知논술/교과서로 논술 잡기]수리영역

《‘교과서에 나오는 심화학습 문제에 통합교과형 논술 대비책이 숨어 있다.’ 서울대 등 주요 대학과 논술 전문가들의 한결같은 주장이다. 교과서를 통해 논술의 기초를 충분히 다질 수 있다는 것이다. 고교 교과서의 핵심 내용을 논술 준비 강의로 진행하는 새 연재를 시작한다. 한 주는 사회와 과학, 한 주는 언어와 수리를 싣는다.》

가능여부를 따져보는 ‘양도논법’

‘비둘기집의 원리’로 규명해보길

□ 집합과 논리(2)

*다음 제시문을 읽고 논제에 답하시오.

(가) 양도논법(兩刀論法)이라 함은, 기본적인 집합의 연산법칙 A∪AB=U 등과 사실상 같은 얘기다. 가령 다음 두 진술이 모두 참이라 해 보자.

① 만약 갑이 범인이라면 을도 범인이다.

② 만약 갑이 범인이 아니라면 을이 범인이다.

우리는 여기에서 갑이 범인인지 아닌지는 알 수가 없다. 하지만 어떤 경우에도(즉, 갑이 범인이건 아니건) 을이 범인이라는 것은 명백하다.

이렇게 따지는 것을 논리학에서는 양도논법이라고 한다.

이 논법은 수학적 사실을 증명할 경우에도 상당히 많이 사용된다.

예를 들어, ‘제곱수 n2을 4로 나눈 나머지는 반드시 0 또는 1이 된다. (단, n은 자연수)’라는 명제를 증명한다고 하자. 우리는 이런 명제를 증명할 경우 n이 홀수일 때와 짝수일 때로 나누어 계산하면 쉽게 증명할 수 있다. 즉,

n=2k+1⇒n2=4k2+4k+1이며, n=2k⇒n2=4k2이다. 임의의 자연수는 홀수이거나 짝수이거나 할 테니까, 이렇게 나누어 증명한다고 하더라도 전혀 일반성을 잃지 않게 된다.

(나) n개의 비둘기집에 n+1마리 이상의 비둘기가 들어갔다면, 두 마리 이상의 비둘기가 들어간 비둘기집이 적어도 하나 있다. 이것은 ‘비둘기집보다 비둘기가 더 많으면 적어도 한 집에는 두 마리 이상 들어 있다’라는 것으로 비둘기집의 원리라 부른다.

실제로 문제풀이에 많이 쓰이는 경우는 ‘n+1마리의 비둘기가 n개의 비둘기집에 들어가려면 적어도 한 집에는 두 마리 이상 들어가야 한다’는 것이다. 만약, 모든 집에 한 마리 이하가 들어간다면 비둘기의 총수는 n마리 이하이므로 처음에 생각한 n+1마리가 될 수 없기 때문이다. 이 원리를 디리클레의 서랍 원리(Dirichlet drawer principle)라고도 한다.

이런 비둘기집의 원리는 다양한 주제에서 풀이의 해법으로 사용되고 있다.

한 예로 머리카락의 수가 같은 사람이 지구상에 존재하는가라는 질문에 대해 이 비둘기집의 원리를 이용하여 설명해보자.

사람의 머리카락은 보통 15만 개를 넘지 않기 때문에, 특이하게 머리카락이 많은 사람을 가정하더라도 100만 개 이상의 머리카락을 가진 사람은 없다고 볼 수 있다. 그런데 전 세계 인구는 60억 명 이상이기 때문에, 머리카락 0개 가진 사람이 한 명, 머리카락을 1개 가진 사람이 한 명… 이런 식으로 헤아려가다 보면, 모든 사람의 머리카락 수가 다르다고 할 경우, 100만 명 정도 헤아릴 수 있고, 이를 넘어서면 어쩔 수 없이 같은 머리카락 수를 가진 사람이 존재할 수밖에 없다. 즉 비둘기집의 원리에 따라 같은 수의 머리카락 수를 가진 사람은 반드시 존재할 수밖에 없다.

□ 논제

<논제1>

갑, 을, 병, 정, 무 다섯 사람은 도둑질을 하다 잡혔다. 하지만 이 중에 진범은 한 명뿐이고, 나머지 사람은 그저 방조한 것에 불과했다. 그래서 취조를 하여 다음의 진술들을 얻어냈다.

갑: 내가 진범이라고 말하는 사람이 있는데, 그것은 거짓말이다.

을: 진범은 ‘무’이다.

병: 나는 진범이 아니다.

정: 진범은 ‘갑’이다.

무: 진범은 ‘정’이다.

이 중에 한 사람만이 진실을 말하고 있으며, 나머지는 거짓말을 하고 있음을 알게 되었다.

이때, 진실을 말한 사람은 누구이며, 진범은 누구인지 제시문 (가)의 원리를 이용하여 설명하시오.

<논제 2>

‘오래살기 운동본부’의 세미나에 200명이 참석을 하였다. 이 사람들은 다양한 나이대의 사람들이 포함되도록 참석자들을 초대하였다. 이 사람들 중에는 나이가 같은 사람들이 반드시 존재하게 된다. 그 이유를 제시문 (나)의 원리를 이용하여 설명하시오.

<논제3>

반지름의 길이가 1인 원의 경계 혹은 내부에 4개의 점을 찍으면 4개의 점 중 어느 두 점간의 거리는 √2이하가 되는 경우가 반드시 존재한다. 이 사실을 다음과 같이 증명해 보자.

이 문제는 무턱대고 한 번에 해결하려 하면 잘 해결되지 않지만, 경우를 잘 나누어 생각해 보면 의외로 간단히 해결될 수 있다.

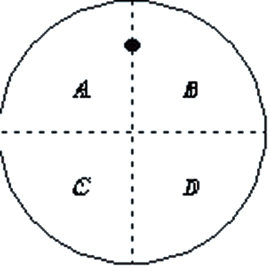
우선 원의 경계 혹은 내부에 1개의 점을 찍고서 그 점과 원의 중심을 연결하는 지름을 긋고, 이 지름과 수직이 되는 지름을 한 개 더 그으면, 오른쪽 그림과 같이 이 원은 4개의 영역으로 나누어진다.

이때 첫 번째 점과 이웃하는 영역을 A, B라 하고 그렇지 않은 영역을 C, D라고 하자. 이제 3개의 점을 어떻게 찍건 결국 4개의 점 중 어느 두 점간의 거리는 √2이하가 되는 경우가 반드시 존재함을 보이는 일만 남았다.

제시문 (가), (나)에 있는 원리를 모두 이용하여 위의 증명을 완결 지으시오.

<논제4>

오른쪽 그림은 A, B, C, D, E, F 6명의 사람을 꼭짓점으로 나타내고, 이 꼭짓점 사이를 변으로 모두 이은 그림이다. 이때, 변은 두 사람이 서로 아는 사이면 굵은 선으로, 서로 모르는 사이면 점선으로 나타내자. 어느 한 꼭짓점 A에 연결된 변 가운데 굵은 선과 점선의 개수에 대하여 제시문 (가), (나)의 원리를 모두 이용하여 다음 사실이 성립함을 논술하시오.

‘6명의 사람이 모이면 항상 그들끼리 서로를 모두 아는 3명이 존재하거나 서로를 전혀 모르는 3명이 존재한다.’

□ 출제 의도

어떤 상황을 논리적으로 파악하여 처리하는 구체적인 방법을 익히기 위한 훈련으로서, 먼저 가능한 경우를 나누어 차근차근 하나하나 따져보는 방법인 ‘양도논법’을 소개하고, 이어서 논리적으로 생각하는 방법 중의 하나인 ‘비둘기집의 원리‘를 이용하는 방법을 익히는 것이 목적이다.

☞ 예시답안은 이지논술 홈페이지에 있습니다

김기철 청솔 아우름 통합논술 수리팀 대표