[理知논술/수학 오디세이]과일 쌓기와 케플러의 추측

과일가게에 가면 둥그런 과일들을 정사면체 모양으로 쌓아 올린 것을 쉽게 볼 수 있다. 이것이 최적의 쌓기라는 것은 굳이 수학을 빌리지 않아도 누구나 알고 있다. 하지만 수학자들은 뻔해 보이는 문제에 대해서도 명확한 답변을 요구하는 경우가 있다. 과일을 정사면체 모양으로 쌓아 올리는 것이 최적이라는 이 분명하고도 하찮은 사실이 바로 ‘케플러의 추측’이라는 유명한 수학문제이다.

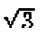
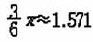
○ 과일을 정사면체로 쌓는 것이 최적의 방법

이 문제는 영국의 항해 전문가인 월터 랠리 경으로부터 시작되었다. 그는 1590년대 말 항해하기 위해 배에 짐을 싣던 중 자신의 조수였던 토머스 해리엇에게 배에 쌓여 있는 포탄 무더기의 모양만 보고 그 개수를 알 수 있는 공식을 만들라고 했다. 그래서 뛰어난 수학자였던 해리엇은 특별한 모양의 수레에 쌓여 있는 포탄의 개수를 알 수 있는 간단한 표를 만들었다. 해리엇은 특정 형태로 쌓여 있는 포탄의 개수를 계산하는 공식을 고안했을 뿐만 아니라, 배에 포탄을 최대한 실을 수 있는 방법을 찾으려고 했다. 그러나 그는 자신이 이 문제를 해결할 수 없다고 생각하여, 당시 최고의 수학자이자 천문학자인 요하네스 케플러에게 편지를 보냈다.

케플러는 이것과 관련된 문제를 1611년 자신의 후원자인 존 와커에게 헌정한 ‘눈의 육각형 결정구조에 관하여’라는 논문에서 처음으로 거론했다. 여기에서 케플러는 평면을 일정한 도형으로 채우는 문제를 생각했다. 평면을 완전하게 채울 수 있는 가장 간단한 도형은 정삼각형이라는 사실로부터 케플러의 문제를 들여다보자.

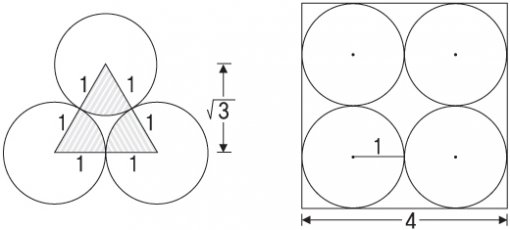
100원짜리 동전 여러 개를 평평한 탁자 위에 올려놓고 이리저리 움직여 붙여 보자 . 동전의 밀도 즉, 전체 공간에 대해 동전이 차지하는 공간의 비율을 가장 높게 배열하는 방법은 동전들이 6개의 서로 다른 동전들로 둘러싸도록 하는 것이다. 따라서 동전들을 정육각형 형태로 규칙적으로 배열하면 평면을 덮을 수 있다. 각 정육각형의 일부는 원이 차지하고 있고, 일부는 빈 공간으로 남아 있다. 정육각형은 정삼각형으로 분할할 수 있기 때문에 삼각형의 밀도를 계산하기만 하면 이 배열의 밀도를 구할 수 있다. 사실 이것을 구하는 것은 삼각형의 넓이와 원의 넓이를 구하는 방법을 알기만 하면 된다.

○ ‘케플러의 추측’ 400년 만에 겨우 증명

계산의 편의를 위하여 100원짜리 동전의 반지름을 1이라고 하면, 평면을 합동인 정삼각형으로 덮을 수 있기 때문에 삼각형 하나만 살펴 보면 충분하다. 동전 3개가 모일 때 그 중심을 연결하면 한 변의 길이가 2인 정삼각형이 된다. 피타고라스의 정리를 이용하여 정삼각형의 높이를 구하면

이므로 정삼각형의 넓이는

이다.

밀도는 정삼각형에서 원으로 덮인 부분을 전체 삼각형의 넓이로 나눈 것이다. 세 원의 6분의 1이 삼각형에 포함되어 있고, 그 부분이 모두 3개이므로 삼각형에 포함되어 있는 부분의 넓이는

이다. 그리고 원으로 덮인 부분을 전체 삼각형 넓이로 나누면 밀도

를 얻는다. 즉, 평면의 약 90.7% 가 동전으로 덮인다. 동전을 정사각형 배열로 하여 평면을 덮는 경우는 약 78.5%를 덮을 수 있다.

케플러는 물질을 구성하는 작은 입자들의 배열 상태를 연구하던 중에 부피를 최소화하려면 입자가 어떻게 배열해야 할지를 생각했다. 모든 입자가 공과 같은 구형이라고 한다면 어떻게 쌓는다 해도 사이사이에 빈틈이 생긴다. 문제는 이 빈틈을 최소한으로 줄여서 쌓인 공이 차지하는 부피를 최소화하는 것이다. 이 문제를 해결하기 위해, 케플러는 다양한 방법에 대하여 그 효율성을 일일이 계산해 보았지만, 끝내 결론을 내리지 못하고 추측만을 남겨 놓게 되었다. ‘케플러의 추측’은 약 400년 동안이나 수학자들을 괴롭히다가 결국 1998년에 미국 미시간대의 토머스 해일스가 증명했다. 그러나 엄밀한 수학적 방법만을 사용한 것이 아니고 상당 부분을 컴퓨터에 의존했다. 세계적인 베스트셀러 ‘페르마의 마지막 정리’의 저자인 사이먼 싱은 ‘케플러의 추측’을 이렇게 평가했다.

“페르마의 마지막 정리를 이을 만한 문제는 그에 못지않은 흥미로움과 매력을 지니고 있어야 한다. ‘케플러의 추측’이 바로 그와 같은 문제이다. 단순해 보이지만 풀려고 하면 결국 문제의 어려움에 압도당하고 만다.”

가끔 수학자들이 어리석은 것은 기실 이와 같은 문제들은 일상생활에 별 도움을 주지 못한다는 것이다.

이광연 한서대 수학과 교수