상훈: 추석에는 할머니, 할아버지도 뵙고 오랜만에 고모와 사촌들을 만날 수 있어서 정말 좋아요. 그런데 뉴스를 보니 연휴 동안 쌓인 쓰레기가 점점 늘어나고 있다고 하더라고요.
엄마: 맞아. 우리 집 주변에도 연휴 기간에 쌓인 각종 선물세트 박스와 음식물 쓰레기가 참 많더라.
엄마: 지금도 예전보다 선물 포장이 많이 간소화되긴 했지. 하지만 아직도 여전히 배송의 편리함이나 내용물의 안전성을 위해서 포장은 필요한 것 같아. 포장을 아예 안 할 수는 없겠지만, 포장용지를 줄이는 방법은 생각해 볼 수 있단다. 수학에서는 포장과 관련해 여러 해결 방안이 제기되기도 했거든. 최근 한 연구를 보니 포장용지를 줄이는 데 유용한 아이디어를 얻을 수 있겠더구나.
○ 종이 자르기의 마술, 테셀레이션
종이는 생활, 예술 분야에서 다양하게 활용되고 있습니다. 종이를 잘 접으면 동물이나 바구니 형태의 입체 모형을 만들 수 있고, 잘 자르기만 해도 평면에 아름다운 장식의 무늬 작품을 만들 수 있죠. 팝업이라는 기법을 통해 입체 책과 같은 재미있는 효과를 만들어 내기도 합니다.
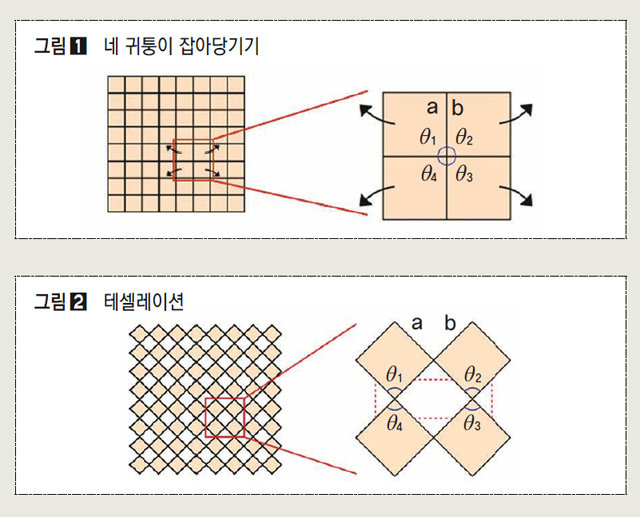
같은 양의 종이라도 잘만 자르면 넓은 면에 붙일 수 있습니다. 포장용지의 면적을 줄일 수 있는 대표적인 방법이죠. 예를 들어 봅시다. 다음과 같이 종이를 8×8개의 작은 정사각형의 격자가 되게 일정한 간격으로 잘랐습니다. 작은 정사각형의 각 꼭짓점은 서로 연결되어 있다고 합시다. 이를 그림과 같이 네 귀퉁이에서 잡아당기면 정사각형 사이에 다시 정사각형의 빈 공간이 생깁니다. ▶그림 [1], [2]
이때 수학적으로 중요한 사실은, 처음 자른 종이가 가지고 있던 성질이 그대로 유지된다는 것입니다. 패턴의 잘라진 선에서 이웃한 두 변의 길이는 서로 같습니다. 또 한 꼭짓점에서 네 조각으로 나누어진 네 내각의 합이 360도인 것도 알 수 있습니다.
○ 사각형 종이로 다양한 도형 덮기
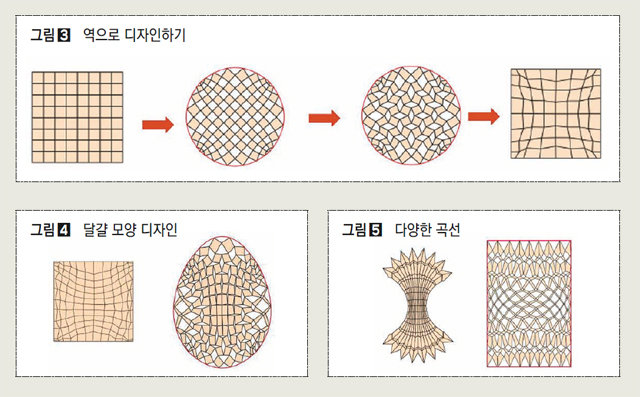
예를 들어 정사각형 종이를 원 모양이 되도록 자르는 방법을 찾는다고 해봅시다. 그러면 처음에는 원이 아닌 직각으로 구성된 정사각형 모양을 생각해야 합니다. 그리고 이웃하는 두 변의 길이와 잘린 네 조각의 내각의 합이 같도록 유지하면서 원 모양에 꼭 맞도록 각 정사각형을 조금씩 변형하는 거죠. 처음 모양을 계속 바꿔 원의 둥근 경계부분이 만들어지도록 합니다. 마지막으로 각 조각을 수축하듯 사각형으로 만들어 주면, 원모양으로 자를 수 있는 패턴이 완성되는 겁니다. 순서만 바꿨을 뿐인데 문제 해결법을 찾아낸 좋은 예라고 할 수 있습니다. 원 모양을 최적화하는 과정은 컴퓨터로 해결하면 더 손쉽게 할 수 있습니다. 몇 가지 계산과 알고리즘을 통해 가능하죠. ▶그림 [3]
이 밖에 달걀 모양을 만들 수도 있습니다. 정사각형이 아닌 종이를 자르면 더 다양한 곡선을 만들 수도 있죠. 반대로 곡선 모양의 도형을 잘라 직사각형을 만드는 방법도 있습니다. ▶ 그림 [4], [5]
쓰레기를 줄이는 데 왕도는 없습니다. 불필요한 물품의 소비를 줄여야 하죠. 오늘 배운 것처럼 수학적 접근으로 쓰레기를 줄일 수 있는 방법을 잘 고민해볼 필요가 있습니다. 여러분도 쓰레기 문제를 수학으로 접근해 새로운 개념의 재활용품 분리수거 방식을 만들어 보면 어떨까요?
박지현 반포고 교사
-
- 좋아요
- 0개
-
- 슬퍼요
- 0개
-
- 화나요
- 0개
-
- 추천해요
- 개
지금 뜨는 뉴스
-
![“연봉 251만 달러, CEO 삼고초려는 기본”… 전세계 AI 인재 확보 비상 [글로벌 포커스]](https://dimg.donga.com/a/464/260/95/1/wps/NEWS/FEED/Donga_Home_News/124678337.1.thumb.jpg)
-

외신 “돈 되는 K팝 산업, 권력투쟁 수렁에 빠져”
- 좋아요 개
- 코멘트 개
-
![숨은 ‘샤이 패밀리스트’ 청년을 찾아라[이미지의 포에버 육아]](https://dimg.donga.com/a/464/260/95/1/wps/NEWS/FEED/Donga_Home_News/124675808.1.thumb.jpg)
숨은 ‘샤이 패밀리스트(Shy Familist)’ 청년을 찾아라[이미지의 포에버 육아]
- 좋아요 개
- 코멘트 개



댓글 0