공유하기
[신문과 놀자!/눈이 커지는 수학]스스로 학습하는 ‘딥러닝’에도 수학 공식이 숨어있어요
- 동아일보
-
입력 2021년 1월 20일 03시 00분
글자크기 설정
이차함수부터 확률과 통계까지
‘AI 이미지’ 분석에 반드시 필요
신산업 분야의 핵심인 ‘인공지능’
고교 수학 과목으로 도입해요

특허청은 디지털 신산업 분야에서 우리 기업들이 국내외 특허를 쉽게 확보할 수 있도록 ‘디지털 신산업 분야 특허 부여 기준’을 만들었다고 18일 밝혔습니다. 디지털 신산업 분야는 인공지능(AI), 사물인터넷(IoT) 서비스, 바이오 등의 5대 핵심 분야를 의미합니다. 특허청은 기존 5대 분야 외에 자율주행, 지능형 로봇, 화장품 등 향후 성장 가능성이 높은 디지털 신산업 분야를 추가 발굴해 기업들이 필요로 하는 맞춤형 특허 부여 기준을 제공할 예정입니다.
○ 스스로 학습하는 딥러닝
이 가운데 인공지능은 최근 정보기술(IT) 업계의 큰 이슈입니다. 인공지능에 이용하는 대표적인 이론이 ‘딥러닝(Deep Learning)’입니다. 컴퓨터와 수학의 세계에서 사물의 모양을 인식하는 것을 패턴 인식이라고 합니다. 이전에는 ‘□□’라는 사물의 패턴 인식을 구현할 때 ‘□□는 ○○의 특징이 있는 것’으로 가르쳤습니다. 하지만 이는 큰 성공을 거두지 못했습니다. 같은 종류라도 색과 모양이 다르고 일정하지 않기 때문에 다양한 이미지에서 특정 개체의 특징을 정확히 인식하는 것은 불가능했습니다.
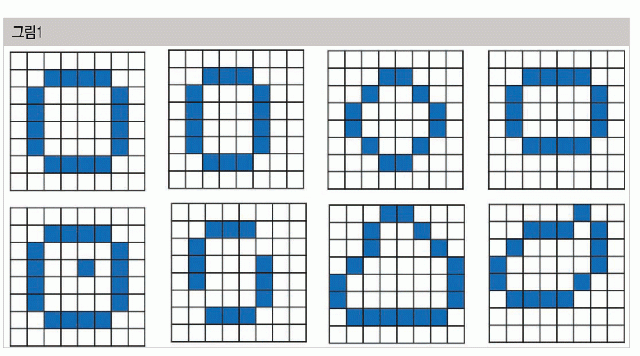
예를 들어 ‘그림 1’과 같이 8×8 픽셀의 필기체 숫자 이미지에서 숫자 0을 인식하고 판별하는 알고리즘을 만든다고 생각해 봅시다. 그림 1의 윗부분에 나타난 4개의 이미지는 크기와 모양이 다르지만 모두 숫자 0입니다, 그런데 ‘0은 이런 형태’라고 컴퓨터에 알려주기에는 아래 4개 이미지는 일관성이 없습니다. 사람은 아래에 있는 4개도 어떻게 하든 0이라고 판별하겠지만 컴퓨터에 이 판독 조건을 가르치기란 쉽지 않습니다.
○ ‘AI 이미지 분석’ 속의 수학
뉴런은 다른 뉴런에서 오는 신호를 수상돌기라고 부르는 입력기를 통해 신경세포 본체에 전달합니다. 뉴런 본체는 여러 뉴런에서 온 입력 신호를 합쳐 여기에 반응할지를 판단합니다.
뉴런은 입력 신호를 받아 그 합을 구하는데, ‘임계값’으로 불리는 의미 있는 수치를 넘으면 받은 신호를 전달합니다. 하지만 그 값을 넘지 않으면 신호를 무시하고 반응하지 않습니다.
뉴런의 반응 여부는 다른 뉴런의 입력신호의 합으로 판단한다고 했는데, 단순하게 y=x1+x2+x3와 같은 식으로 표현할 수 있는 것은 아닙니다. 몇 가지 더 고려할 것이 있는데 그중 하나가 각각의 신호가 가진 정보를 판단하는 데 유용한 결합 정도에 따라 각 입력신호 변수에 곱해주는 가중치라는 값입니다. 보통 w를 쓰고, 각 변수마다 이름을 붙여 w1, w2, w3 등으로 나타냅니다. 또 반응 여부를 결정하는 특정한 경계값을 θ라고 하면 반응신호에 대한 식은 다음과 같이 나타낼 수 있습니다.
출력신호 없음(y=0): w1x1+w2x2+w3x3<θ
출력신호 있음(y=1): w1x1+w2x2+w3x3 ≥θ
이와 같이 생각하면 생물학적 뉴런의 반응 여부에 따라 출력신호는 y=0 또는 y=1로 표현됩니다. 그러나 생물학적 조건을 주지 않으면 굳이 0, 1로만 표현하지 않아도 됩니다. 그래서 수학적으로는 특정 값에 영향을 받지 않는 함수 α로 바꾸어 표현하여 y를 0과 1로 한정 짓지 않고 다음과 같이 나타냅니다.
이때 α라는 함수를 활성화 함수라 하고, 대표적으로 시그모이드 함수가 사용됩니다. 그 외에도 신경망 모델이 정보를 잘 설명하면서 다루기 편하도록 다양한 함수들이 만들어져 활용되고 있고, 이러한 함수식을 다루는 데는 우리가 중고등학교에서 배우는 일차, 이차함수에서부터 수열, 미분, 확률과 통계, 벡터 등의 내용이 필수적으로 필요합니다.
○ 인공지능 교육과정의 도입
인공지능을 이용한 이미지 분석은 많은 분야에서 각광받고 있습니다. 제조 공장에서 제품 불량 여부를 스스로 판별하는 스마트팩토리, 질병을 예측하고 분석하는 의료 서비스, 보안검색 등 다양한 분야에서 활용됩니다. 교육부는 2025년부터 초중고 교육과정에 새로 ‘인공지능’을 도입한다고 밝혔습니다. 또 2021년부터는 고등학교 수학 진로선택 과목으로 ‘인공지능 수학’이 도입됩니다. 그만큼 인공지능과 수학이 관련이 있다는 이야기겠지요?
박지현 반포고 교사
트렌드뉴스
-
1
부부 합쳐 6차례 암 극복…“내 몸의 작은 신호 잘 살피세요”
-
2
덴마크 언론 “폭력배 트럼프”… 英국민 67% “美에 보복관세 찬성”
-
3
[이진영 칼럼]잘난 韓, 못난 尹, 이상한 張
-
4
“하루 3분이면 충분”…헬스장 안 가도 건강해지는 ‘틈새 운동’법
-
5
김정은, 공장 준공식서 부총리 전격 해임 “그모양 그꼴밖에 안돼”
-
6
결국 날아온 노란봉투…금속노조 “하청, 원청에 교섭 요구하라”
-
7
82세 장영자, 또 사기로 실형…1982년부터 여섯 번째
-
8
단순 잇몸 염증인 줄 알았는데…8주 지나도 안 낫는다면
-
9
강선우 “원칙 지키며 살아”… 前보좌관 “강선우 1억 받아 전세금 보태” 진술
-
10
‘오들오들’ 북극한파에 치솟는 혈압…‘이것’ 꼭 실천해야
-
1
李대통령 “제멋대로 무인기 침투, 北에 총 쏜 것과 똑같다”
-
2
李대통령 “생리대 고급화하며 바가지…기본 제품 무상공급 검토”
-
3
‘평양 무인기 침투’ 尹 계획 실행한 드론사령부 해체된다
-
4
강선우, 의혹 22일만에 경찰 출석…“원칙 지키는 삶 살았다”
-
5
정청래 “비법률가인 나도 법사위원장 했다”…검사 권한 고수 비판
-
6
李 가덕도 피습, 정부 공인 첫 테러 지정…“뿌리를 뽑아야”
-
7
[속보]李대통령 “무인기 침투, 北에 총 쏜 것과 똑같다”
-
8
홍준표 “과거 공천 헌금 15억 제의받아…김병기·강선우 뿐이겠나”
-
9
“장동혁 죽으면 좋고” 김형주 막말에…국힘 “생명 조롱”
-
10
의사 면허 취소된 50대, 분식집 운영하다 극단적 선택
트렌드뉴스
-
1
부부 합쳐 6차례 암 극복…“내 몸의 작은 신호 잘 살피세요”
-
2
덴마크 언론 “폭력배 트럼프”… 英국민 67% “美에 보복관세 찬성”
-
3
[이진영 칼럼]잘난 韓, 못난 尹, 이상한 張
-
4
“하루 3분이면 충분”…헬스장 안 가도 건강해지는 ‘틈새 운동’법
-
5
김정은, 공장 준공식서 부총리 전격 해임 “그모양 그꼴밖에 안돼”
-
6
결국 날아온 노란봉투…금속노조 “하청, 원청에 교섭 요구하라”
-
7
82세 장영자, 또 사기로 실형…1982년부터 여섯 번째
-
8
단순 잇몸 염증인 줄 알았는데…8주 지나도 안 낫는다면
-
9
강선우 “원칙 지키며 살아”… 前보좌관 “강선우 1억 받아 전세금 보태” 진술
-
10
‘오들오들’ 북극한파에 치솟는 혈압…‘이것’ 꼭 실천해야
-
1
李대통령 “제멋대로 무인기 침투, 北에 총 쏜 것과 똑같다”
-
2
李대통령 “생리대 고급화하며 바가지…기본 제품 무상공급 검토”
-
3
‘평양 무인기 침투’ 尹 계획 실행한 드론사령부 해체된다
-
4
강선우, 의혹 22일만에 경찰 출석…“원칙 지키는 삶 살았다”
-
5
정청래 “비법률가인 나도 법사위원장 했다”…검사 권한 고수 비판
-
6
李 가덕도 피습, 정부 공인 첫 테러 지정…“뿌리를 뽑아야”
-
7
[속보]李대통령 “무인기 침투, 北에 총 쏜 것과 똑같다”
-
8
홍준표 “과거 공천 헌금 15억 제의받아…김병기·강선우 뿐이겠나”
-
9
“장동혁 죽으면 좋고” 김형주 막말에…국힘 “생명 조롱”
-
10
의사 면허 취소된 50대, 분식집 운영하다 극단적 선택
-
- 좋아요
- 0개
-
- 슬퍼요
- 0개
-
- 화나요
- 0개

댓글 0