

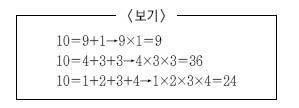

2. [확률과 통계]
3. [문자와 식] 귤이 들어 있는 상자가 9개 있습니다. 이 상자 가운데 귤의 개수가 가장 많은 것은 55개이고, 가장 적은 것은 50개입니다. 9개의 상자에 들어 있는 귤을 모두 꺼내어 다른 상자에 40개씩 나누어 담으면 마지막 상자에는 14개의 귤이 모자란다고 합니다. 9개의 상자에 들어 있는 귤은 모두 몇 개입니까?
4. [수와 연산] ㉮와 ㉯ 두 사람이 어떤 건물에 페인트를 칠하기로 하였습니다. 두 사람이 함께 일한 5일 동안에는 건물 전체의 5/8만큼 칠했고, 9일 동안에는 ㉮ 혼자서 나머지를 칠했습니다. 만약 처음부터 ㉯ 혼자서 페인트를 칠했다면 며칠이 걸렸겠습니까? 단, ㉮, ㉯ 각자의 일하는 속도는 일정합니다.
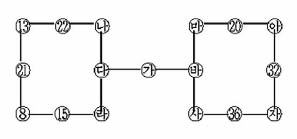
7. [규칙성과 함수] 다음은 ─에 └모양의 선을 계속해서 그려나가는 그림입니다. 100번째 그림에 나타나는 선끼리 만나는 점의 개수를 ㉠이라 하고 가장 작은 사각형의 개수를 ㉡이라고 할 때, ㉠―㉡의 값은 얼마입니까?
8. [문자와 식] 참외는 5개에 4000원이고 토마토는 6개에 3000원입니다. 참외와 토마토를 섞어서 낱개로 15개를 골랐더니, 주인이 200원을 깎아서 10000원만 달라고 했습니다. 참외를 몇 개 샀는지 구하시오.
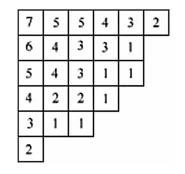
9. [통합형 심층] 다음은 한 직선 위의 세 수를 (가운데의 수)=(양쪽의 두 수의 합)이 되도록 만든 그림입니다. 이 그림에서 ㉮에 들어갈 수는 얼마입니까?
10. [통합형 심층] 다음 <보기>는 10을 두 개 이상의 자연수의 합으로 나타낸 후, 그 자연수들의 곱을 구한 것입니다. <보기>와 같은 방법으로, 더하여 11이 되는 수들을 모두 곱한 수 중에서 가장 큰 수는 얼마입니까?
▶easynonsul.com에 동영상강의
시도교육청·대학부설 영재교육원 초등부 선발시험 대비 문제(3∼5학년) 해설 및 정답은 인터넷 이지논술 사이트(www.easynonsul.com)에서 볼 수 있습니다.
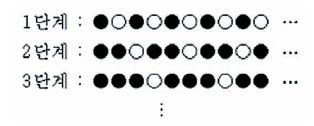
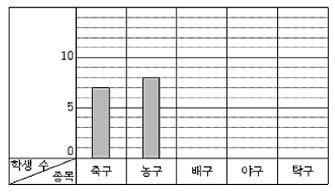
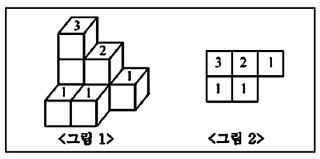
Tip. 각 단계별 흰색 구슬의 자리를 수로 나타내 보세요. Tip. 남은 20명의 학생 중 배구를 좋아하는 학생은 8명보다 많고, 탁구를 좋아하는 학생은 배구를 좋아하는 학생 수보다 적어야 합니다. Tip. 귤의 개수가 가장 많은 경우와 가장 적은 경우로 나누어 귤의 개수가 될 수 있는 범위를 생각해보세요. Tip. 함께 일한 5일 동안의 일의 양에서 ㉮와 ㉯가 함께 하루 동안 한 일의 양을 구할 수 있어요. Tip. 8개를 덜어낸 입체도형을 머릿속에 그려보고, 덜어내서 들어간 부분에는 몇 개의 면이 있는지 세어 보세요. Tip. 입체도형의 가장 바깥쪽 쌓기 나무를 제외한 후 생각합니다. 색칠이 안 되려면 주위에 자신보다 높거나 같은 높이로 쌓기 나무가 쌓여야 합니다. Tip. 만나는 점의 개수와 가장 작은 사각형의 개수는 일정한 규칙에 따라 증가합니다. Tip. 참외와 토마토의 개수를 예상하여 계산한 후, 실제 지불해야 하는 금액과의 차이를 확인하여 답을 구해 보세요. Tip. 오른쪽 사각형의 글자와 수로 덧셈 식을 만들어 식을 비교하면 ㉳의 값을 구할 수 있어요. Tip. 곱이 큰 수를 구하기 위해서는 1이 포함되지 않는 식으로 만들어야 합니다. 합을 이루는 자연수의 개수에 따라 각 경우의 곱을 구해 보세요.
-
- 좋아요
- 0개
-
- 슬퍼요
- 0개
-
- 화나요
- 0개
-
- 추천해요
- 개
지금 뜨는 뉴스
-

푸틴 러 대통령, 5월에 中 방문 계획…대선 이후 첫 해외 방문
- 좋아요 개
- 코멘트 개
-
![첫 회의서 ‘용산 비서들 정치 행위’ 근절 강조한 정진석[횡설수설/김승련]](https://dimg.donga.com/a/464/260/95/1/wps/NEWS/FEED/Donga_Home_News/124662945.1.thumb.jpg)
[횡설수설/김승련]첫 회의서 ‘용산 비서들 정치 행위’ 근절 강조한 정진석
- 좋아요 개
- 코멘트 개
-
![‘AI 3대 강국’ 외치더니 패싱당한 한국[오늘과 내일/김재영]](https://dimg.donga.com/a/464/260/95/1/wps/NEWS/FEED/Donga_Home_News/124662979.1.thumb.jpg)
[오늘과 내일/김재영]‘AI 3대 강국’ 외치더니 패싱당한 한국
- 좋아요 개
- 코멘트 개
댓글 0