[理知논술/교과서로 논술 잡기]수리영역

코흐의 눈송이를 한없이 그려나갈때 그 넓이의 규칙성은?

■ 주제: 수열의 극한의 활용(2)-무한급수

※ 다음 제시문을 읽고 논제에 답하시오.

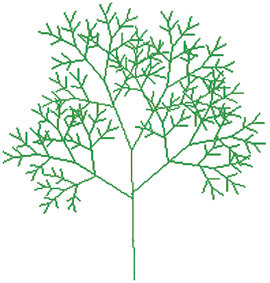
(가) 주변의 나무 모습을 살펴보면 나무 위로 떨어지는 햇빛을 조금이라도 낭비하지 않고 광합성에 이용할 수 있도록 나뭇잎이 조금도 빈틈없이 나무 전체를 뒤덮고 있음을 알 수 있다.

나뭇잎이 이렇게 나무 전체를 뒤덮기 위해서는 나무의 잔가지들이 모든 방향으로 골고루 나 있어야 한다. 그렇다면 과연 나무의 무엇이 잔가지들의 방향을 통제하여 모든 방향으로 골고루 향하도록 해줄까? 복잡하게 얽힌 나뭇가지를 보면서 나뭇가지의 기하학적 구조가 매우 복잡할 것이라고 생각할 수가 있다.

글 싣는 순서(수리)
1	집합과 논리 (1)
2	집합과 논리 (2)
3	수와 식 (1)
4	수와 식 (2)
5	수와 식 (3)
6	도형과 문제 해결 (1)
7	도형과 문제 해결 (2)
8	함수의 활용 (1)
9	함수의 활용 (2)
10	함수의 활용 (3)
11	지수·로그의 실생활 응용 (1)
12	지수·로그의 실생활 응용 (2)
13	행렬의 실생활 응용 (1)
14	행렬의 실생활 응용 (2)
15	수열과 추론 (1)
16	수열과 추론 (2)
17	수열과 추론 (3)
18	수열의 극한의 활용 (1)
19	수열의 극한의 활용 (2)
20	경우의 수란 무엇인가?
21	확률의 활용 (1)
22	확률의 활용 (2)
23	통계의 허와 실 (1)
24	통계의 허와 실 (2)

그러나 사실 이런 나뭇가지의 형태는 매우 간단한 규칙으로부터 만들어진다. 나뭇가지가 일정한 길이의 비(比)가 될 때마다 두 개의 가지로 갈라진다고 하는 간단한 규칙만으로도 모든 방향으로 뻗은 나뭇가지의 구조를 만들어 낼 수가 있다.

이 경우에 가지의 어느 부분을 선택하여 확대를 해도 전체 나무 모양과 같은 모양을 얻을 수 있다. 이러한 성질을 ‘자기 유사성(Self-Similarity)’이라고 하며, 자기 유사성을 갖는 기하학적 구조를 프랙털 구조라고 한다.

허파에서 동맥이 갈라져서 실핏줄을 이루는 구조 역시 프랙털 구조의 예이다. 허파로 들어오는 하나의 동맥은 계속 갈라져서 공기와 실핏줄의 접촉면을 최대로 하여 가장 효율적으로 산소 교환이 일어날 수 있도록 하는 허파꽈리를 형성하게 되는 것이다.

(나) 프랙털은 카오스에 내재한 질서 구조이자 그것을 묘사할 수 있는 언어라고 할 수 있으며, 카오스가 복잡하면서도 그 속에 하나의 질서를 지니는 것은 프랙털이 있기 때문이다. 프랙털은 고사리처럼 부분이 전체를 닮은 모양을 하고 있으면서(자기 유사성), 이런 닮는 과정을 끊임없이 반복하는(순환성) 특징을 지니고 있다.

그 외에도 고사리와 같은 양치류 식물, 아름다운 눈송이의 구조, 우주의 신비스러운 모습, 하천의 흐름, 산맥의 지형, 너울이 밀려오는 해안선의 모습, 새하얀 뭉게구름의 형상 등 주변의 많은 것들에서 우리는 프랙털 구조를 쉽게 발견할 수가 있다. 그러나 이 세상에서 완전히 똑같은 것은 없다. 다만 우리가 같은 유(類)에 관한 자기닮음을 직관적으로 인식하기에 같은 것으로 보이는 것이다.

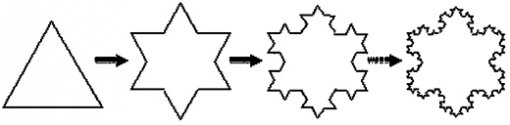
‘코흐 곡선’은 수학의 곡선으로 가장 처음에 나온 프랙털 도형 중 하나이다. 1904년 스웨덴의 수학자 코흐의 논문에 처음 등장하여 그런 이름이 붙었다. 시작하는 도형이 정삼각형인 경우 ‘코흐 눈송이’라 하고 다음과 같이 만든다.

1. 정삼각형을 그린다.

2. 각 변을 3등분해서, 한 변의 길이가 이 3등분의 길이와

같은 정삼각형을 붙인다.

3. 2의 과정을 반복한다.

이 과정을 통해 얻어진 코흐 눈송이를 그림으로 나타내면 아래의 그림과 같다.

[논제 1] 위의 그림의 도형에서 변의 둘레의 길이로부터 발견할 수 있는 규칙성을 제시하고 둘레의 길이가 무한으로 발산함을 설명해 보아라.

[논제 2] 코흐 눈송이를 한없이 반복하여 그려나갈 때, 그 넓이로부터 발견할 수 있는 규칙성을 제시하고 넓이가 수렴함을 설명해 보아라.

[논제 3] 제시문 (나)를 인용하여 코흐 눈송이가 프랙털의 도형이라는 것을 설명해 보아라.

<출제 취지>

1. 무한등비급수의 합공식을 알고 이를 활용해 보도록 한다.

2. 프랙털 도형에 대한 이해를 통하여 도형의 닮음성에 대하여 생각해 보고 이를 통해 극한값에 대하여 적용하여 무한과 유한이 상반하여 공존하는 값이 존재함을 알게 한다.

<기초 학습>

코흐 눈송이의 한 변은 3등분 된 후 가운데 부분이 자기 복제를 하여 2개가 됨으로써 항상 변의 길이가 4/3배로 늘어난다. 그로인해 각 변에서 넓이는 처음 제시된 도형의 넓이의 1/9이 늘어남을 알 수 있다.

☞ 예시답안은 이지논술 홈페이지(easynonsul.com)에 있습니다.

유재원 청솔 아우름 통합논술 강사