
상훈: 다빈치 특별전이 프랑스 루브르 박물관에서 열린다고 들었어요. 이탈리아 사람 아닌가요?
엄마: 다빈치는 이탈리아 화가이긴 하지만 주요 그림 작품의 많은 수가 프랑스에 있단다. 말년을 프랑스에서 보냈기 때문에 두 나라에서 다 행사를 진행하는 것으로 안단다.
엄마: 그 당시에는 구분이 없었지만 오늘날의 분야로 생각해 보면 회화, 조각, 건축, 수학, 과학, 발명, 해부학, 지질학, 천문학, 정치 등 13∼18개의 전문가로 여겨질 수 있다고 하니 대단한 사람이었지. 그동안 잘 몰랐던 수학자로서의 다빈치를 살펴볼까?
○ 수학과 예술
자연에는 선이 존재하지 않습니다. 단지 인간이 물체와 물체 사이를 명확하게 구별하기 위해 관습적으로 선을 그리는 것입니다. 그는 멀고 가까움을 표현하는 선 원근법을 이용하면서도, 당시의 다른 화가들과는 달리 물체와 물체의 경계를 이루는 윤곽을 선으로 그리지 않았습니다. 보는 사람으로 하여금 그의 머릿속에서 윤곽선이 그려지게 했습니다.
‘최후의 만찬’에서는 이런 선 원근법이 잘 드러납니다. ‘모나리자’가 유명한 것은 마치 살아 있는 사람처럼 볼 때마다 모나리자의 표정이 바뀐다는 점 때문입니다. 모나리자의 그림에는 그 어디에도 윤곽선이 없습니다. 다빈치가 대기 원근법의 원리를 모나리자에 적용했기 때문입니다.
○ 신성한 비례와 황금비

다빈치가 그림으로 표현한 플라톤 입체 연구에서 3차원 물체를 2차원으로 정확하게 나타내려면 미술 원근법을 제대로 이해하고 있어야 했습니다. 다빈치는 파촐리의 신성한 비례를 위해 플라톤 입체 그림을 고쳐 그렸습니다.
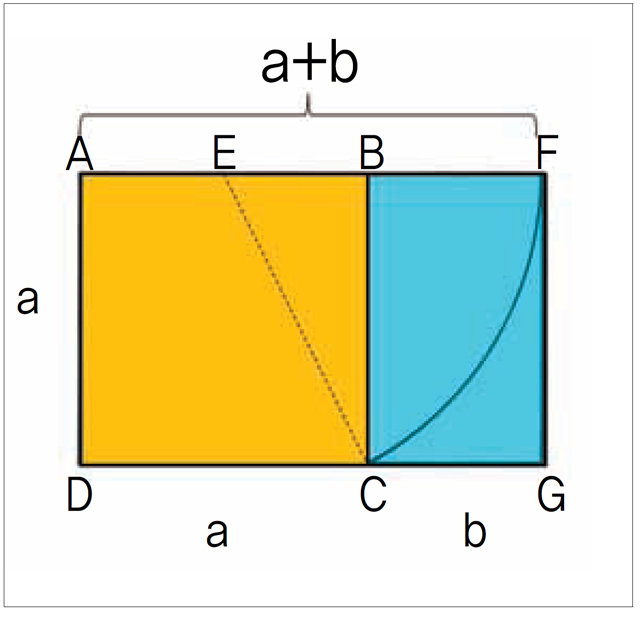
이때 정사각형의 한 변(AB=AD)의 길이를 2라고 하고, 이등분 지점인 중점을 E로 하면 직각삼각형의 성질에 의해 (EC=EF=√5)가 되고, 황금사각형의 두변의 비,
이 값은 약 1.618로, 이를 황금비라고 합니다. 이 수는 무한히 계속되는 소수, 즉 무리수입니다. 황금비는 많은 사람들 사이에 신성한 비율로 여겨졌습니다. 황금비는 자연과 과학은 물론 예술에도 나타납니다. 파르테논 신전, 이집트 피라미드, 모나리자에서 황금비를 찾아볼 수 있습니다.
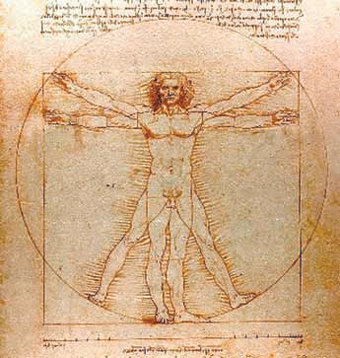
다빈치는 수학에 대한 지식을 사용해 ‘이상적 비율’로 여겨지는 수많은 그림을 그렸습니다. 인간의 비율에 관한 그의 작품 중 하나는 ‘비트루비우스적 인간’(Vitruvian Man)입니다. 그림에서 사람을 둘러싼 정사각형과 원이 보입니다.(그림 참고) 팔을 옆으로 쫙 펼치면 키와 같으니 정사각형을 그리고, 원의 중심은 배꼽입니다. 수학의 사용을 통해 완벽한 인간 형태를 시각적으로 나타냅니다. 인간이 수학 법칙이 설명할 수 있는 완벽한 창조물이라는 믿음에서 온 것이지요.
다빈치는 고대의 인체비례론을 그대로 받아들이지 않고 실제로 사람들을 데려다 실측해 기록했습니다. ‘양팔을 펼친 길이는 키와 같다’, ‘머리카락 끝 선에서 턱 끝까지는 키의 10분의 1이다’ 등의 설명은 그가 신체의 곳곳을 숫자로 계산하면서 사람의 몸을 기하학적 관점에서 계량화하는 고대 사상을 실험한 것입니다. 다빈치의 ‘호기심’과 ‘관찰력’은 우리에게 큰 가르침을 줍니다. 국내에서도 다빈치 관련 강연 등이 진행 중입니다. 그의 다양한 회화와 조소, 공학 작품에서 수학을 찾는 재미를 느껴보기를 바랍니다.
박지현 반포고 교사
박지현 반포고 교사
-
- 좋아요
- 0개
-
- 슬퍼요
- 0개
-
- 화나요
- 0개
-
- 추천해요
- 개
지금 뜨는 뉴스
-

“1억 주면 아이 낳으시겠습니까”…권익위, 국민 의견 듣는다
- 좋아요 개
- 코멘트 개
-

‘봉하·평산’ 찾은 새미래…文 “거대양당 마음 못주는 국민 대변하길”
- 좋아요 개
- 코멘트 개
-

다운증후군 남성이 엘리베이터 타자 끓는 물 뿌린 말레이시아 여성
- 좋아요 개
- 코멘트 개
댓글 0